Solve similar problems

Perhaps the most obvious thing that we can do when presented with a hard problem is to first try to solve a similar, but simpler problem. By solving simpler models we develop techniques and ideas that help us understand the original problem. In the study of polyominoes (arguably) the most successful line of research has been the enumeration of simpler subsets of polyominoes. By enforcing additional restrictions, such as directedness or convexity, the set of polyominoes can be reduced until it is solvable. Many of these similar problems are interesting in their own right. Consider, for example, directed polyominoes (we will describe them in detail in chapter 4). Directed polyominoes must contain a single tile called the root or source from which all the other tiles can be reached by paths taking only north and east steps (see figure 7); this particular model has been solved. Directedness arises naturally in models which are subject to strong forces such as gravity, and can also be used to model time dependence (since objects cannot move backwards in time). Dhar [12,13] showed that certain directed polyomino models are connected to certain gas models. i.e. it is important for reasons other than that it lets us solve the model -- it is not just a consolation prize.

In the next section we list some variations of the basic polyomino problem that have been studied. It should be noted that subclasses of general polyominoes (certainly all the solved subclasses) have smaller growth constants (directed polyominoes have a growth constant 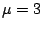$\mu=3$). Part of the challenge of enumerating subclasses is to enumerate large subclasses with growth constants close to those of general polyominoes.

Figure: If there exists a single root cell, from which all the cells of the polyomino can be reached by a directed path, then the polyomino is a directed polyomino.

Let us now examine some of these objects related to polyominoes.