Papyrology is one of the best organized and most pleasantly managed fields of the humanities.
Otto Neugebauer in The Exact Sciences in Antiquity (p. 58).

One of the oldest extant diagrams from Euclid

One of the oldest and most complete diagrams from Euclid's Elements of Geometry is a fragment of papyrus found among the remarkable rubbish piles of Oxyrhynchus in 1896-97 by the renowned expedition of B. P. Grenfell and A. S. Hunt. It is now located at the University of Pennsylvania. The diagram accompanies Proposition 5 of Book II of the Elements, and along with other results in Book II it can be interpreted in modern terms as a geometric formulation of an algebraic identity - in this case, that ab + (a-b)2/4 = (a+b)2/4 (although the relationship between Euclid's propositions and algebra, which he did not possess, is controversial).

Click on the image to see one at much higher resolution.

Contents

What exactly are we looking at?

This is a fragment of what is likely part of a larger papyrus roll from the early years of the current era. It was dated by its original finders to around 300 A.D., but a more recent judgment by Eric Turner places it between 75-125 A.D. It was dug up in 1896-7 from rubbish piles of the ancient town of Oxyrhynchus, near the present village of Behnesa (about 110 miles up the Nile from Cairo and 10 miles west of it), during one of several expeditions financed by the Egypt Exploration Fund (later renamed as the Egypt Exploration Society) and led by B. P. Grenfell and A. S. Hunt of Oxford University. Oxyrhynchus at that time was populated by Greek colonists, a remnant of the conquest in about 330 B. C. by Alexander the Great. It is commonly believed that Euclid himself lived and taught in Alexandria around 300 B.C., but what we know for certain about his life is close to nil.

The fragment contains the statement, in Greek, of Proposition 5 from Book II of Euclid's Elements. At the very top of the fragment is a small trace of what seems to be the statement of Proposition II.4. No part of the proof of either Proposition is present.

The handwriting is in capitals. Words are not separated from each other, and several words are broken in the middle at line ends. There are no diacritical marks. All of this was normal practice in Greek manuscripts of the period. The papyrus is of lower quality than many other texts from the same period. The material itself is rough, the handwriting is not of professional scribal quality, the diagram has been drawn over, and in addition it has no labels to match the reasoning in Euclid's proof. For these reasons it has been conjectured (by David Fowler) that it was written by someone for private use.

Some artefacts of the process of papyrus manufacture are visible in the image - at the upper left you can detect how the sheet of papyrus was made by laying down strips from the stalk of the plant in orthogonal directions, and the vertical line in the centre shows that it was formed by gluing together two separate strips. Normally a full roll was made up by gluing pieces together in this way, and might be about 30 feet long. The ink is a brownish colour, indicating that it was made from nut gall, the common source of ink for manuscripts for several hundred years.

What does the text say?

Here is the complete original report of Grenfell & Hunt:

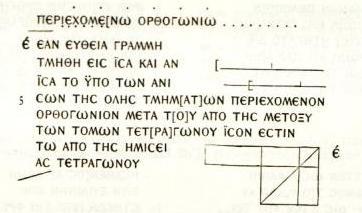
The modern Greek edition of J. L. Heiberg renders II.5 as

It reads in English like this (from the classic translation of T. L. Heath):
If a straight line be cut into equal and unequal segments, the rectangle contained by the unequal segments of the whole together with the square on the straight line between the points of section is equal to the square on the half.

For more information:

  • The Thirteen Books of Euclid's Elements, translated from the text of Heiberg, with introduction and commentary by Thomas L. Heath.
    Available from Dover in three volumes.
  • David Joyce's on-line edition of Heath's translation
    The entire Elements can be found there, with interactive figures.
  • The Perseus project
    This has all of Heath's text, including a version in Greek, but in a less readable format than Joyce's, and also Heath's comments on the significance of the Proposition.
  • The history of Euclid's text.
    Again, the Perseus project. You can also find here a brief mention of the fragment itself in Heath's discussion.
  • The original report of Grenfell and Hunt.
    This is a facsimile of the report in volume I of The Oxyrhynchus Papyri, as well as their transcription into more readable Greek of the exact text. By comparing this transcription with the excerpt from Heiberg's edition above, you can get a good idea of the style in which the papyrus was written - without word breaks, and with broken words, for example.

The Proposition might be made clearer by these pictures, from which you can also see the relationship with the algebraic identity ab + (a-b)2/4 = (a+b)2/4.


How old is this fragment?

Grenfell & Hunt said of it
From the character of its handwriting, which is a sloping rather irregular informal uncial, this papyrus may be assigned to the latter part of the third or the beginning of the fourth century
but after an examination done at the request of David Fowler, the eminent papyrologist Eric Turner wrote
I should date it confidently to the end of century i AD/early century ii, say AD 75-125. ... Note that this text was one of the first finds of Grenfell & Hunt at Behnesa (Oxyrhynchus). They published in a great hurry, and no doubt included this piece to illustrate the wide range of subjects on which papyri could throw light. Their papyrological (especially dating) framework was still to be worked out. By 1902 I do not think the dating offered would have been "third or fourth century."
More of Turner's report is included in The Mathematics of Plato's Academy.

Where is the fragment now?

Although Oxford was the major sponsor of the expedition of Grenfell and Hunt, the University of Pennsylvania had also contributed to its support, and for this reason the University acquired the fragment in 1901. It is now to be found in the storage vaults of the Museum of Archaelogy and Anthropology at the University of Pennsylvania. It is #E2748 in the Museum catalogue.

What other really ancient items from Euclid's Elements are there still around?

Not much from before the ninth century, mostly small fragments like this one. You can find a pretty complete list in Chapter 6 of David Fowler's book The Mathematics of Plato's Academy, which also has a collection of images.

One of the two oldest complete manuscripts is the Greek manuscript D'Orville 301, dated 888 A.D, at the Bodleian Library of Oxford University. A single image from that manuscript is available on-line. The frontispiece of T. L. Heath's translation is from this manuscript, and The Mathematics of Plato's Academy contains an image of two pages concerned with II.5. Incidentally, the manuscript is not normally accessible even to authorized readers at the Library, presumably on account of its fragility, but a micro-film of the full manuscript is available for examination. It is not really of very high quality, I am afraid . (It would be great if the Bodleian would have the whole book photographed and made available on the Internet, wouldn't it?)

The other of the two is at the Vatican.

David Fowler estimates that less than 1% of Euclid's Greek text is available from any source earlier than 888.

What's the 29 doing there?

Presumably written there by Grenfell or Hunt. This is referred to as Oxyrhynchus I.29 because it is number 29 among the published papyri.

More information - on the Internet

More information - texts

  • The Oxyrhynchus Papyri
    The series is still being published by the Egypt Exploration Society (go further to /Publications/Graeco-Roman Memoirs), and early volumes are still available for purchase! A related publication is the book edited by Alexander Jones (Astronomical Papyri from Oxyrhynchus, published by the American Philosophical Society).
  • Leo Deuel, Testaments of Time - the search for lost manuscripts and records, A. Knopf, 1965.
    Chapters 5-10 present a good popular account of the discovery and importance of Egyptian papyri, and Chapters 8-9 discuss in particular the remarkable Oxyrhynchus expeditions of B. P. Grenfell and A. S. Hunt. This was reprinted by Penguin in 1970.
  • David Fowler, The Mathematics of Plato's Academy (second edition). The Clarendon Press, Oxford, 1999.
    Chapter 6 is a fine introduction to papyri in general, along with comments on MS D'Orville 301. This book contains other photographs of early mathematical texts.
  • Arthur S. Hunt, Papyri and papyrology, Journal of Egyptian Archaelogy 1, 1914, pp. 81-92.
    A useful survey article by one of the protagonists in our story.
  • Alfred Lucas, Ancient Egyptian materials and industries, E. Arnold, 1962.
  • Otto Neugebauer, The Exact Sciences in Antiquity, Princeton University Press, 1952.
    A short and classic introduction to ancient science, particularly mathematics and astronomy.
  • Paul Nicholson and Ian Shaw, Ancient Egyptian materials and technology, Cambridge University Press, 2000.
  • Eric G. Turner, Greek Papyri: an introduction. The Clarendon Press, Oxford, 1968.
    A very readable and authoritative book.

Thanks

Jennifer Wegner, one of the keepers of the Egyptian section at the Museum of Archaelogy and Anthropology at the University of Pennsylvania, made the fragment available to me and gave me assistance in photography. The Museum was extremely generous in letting me make and publish the photographs.

The Ha, system administrator in the Department of Mathematics at the University of British Columbia, helped me with image manipulation.

Peter Brown, of the School of Mathematics at the University of New South Wales, helped me with Greek typography in TEX.

David Fowler has helped me enormously. He has suggested extensive corrections to my original text, and made available to me a copy of a letter from Eric Turner to him. Of course he should not be held accountable for errors.

About the images

The photographs were taken in the vaults of the museum at the University of Pennsylvania with a Nikon CoolPix 990 (a digital camera), using a light stand and incandescent lights at the Museum, along with a Benbo tripod for close work.