p-Orbitals
p-Orbitals are
governed by their radial functions and two angular elements. Many of the
principles of radial orbitals for the p-Orbitals are same as in the
s-Orbitals. As such, their angular elements are discussed here. The three equations
for the 2p orbitals are given by:
Y+ = (3/4π)1/2 sin Θ
cos Φ
Y- = (3/4π)1/2 sin
Θ sin Φ
Y0 = (3/4π)1/2 cos
Θ
Each of the
three orbitals has the different radial elements, since two of the
functions depend on Φ and Θ. It will turn out that the three orbitals
are each aligned along a different axis in the Cartesian plane. Using
the Cartesian-Spherical conversion, we use the following conversion formulas:
x = sin Θ cos Φ
y = sin Θ sin Φ
z= cos Θ
we obtain:
Ypx = (3/4π)1/2 sin Θ cos Φ = (3/4π)1/2
x/r
Ypy = Y- = (3/4π)1/2 sin Θ
sin Φ = (3/4π)1/2 y/r
Ypz = (Y0 = (3/4π)1/2 cos Θ = (3/4π)1/2 z/r
This means that
we can graph one function with respect to an axis (x , y, or z), and
then rotate 90° to the other two axes, and we have a full set of p
orbitals.The
angular element is given by cos Θ. We graph in polar
co-ordinates on a polar grid:
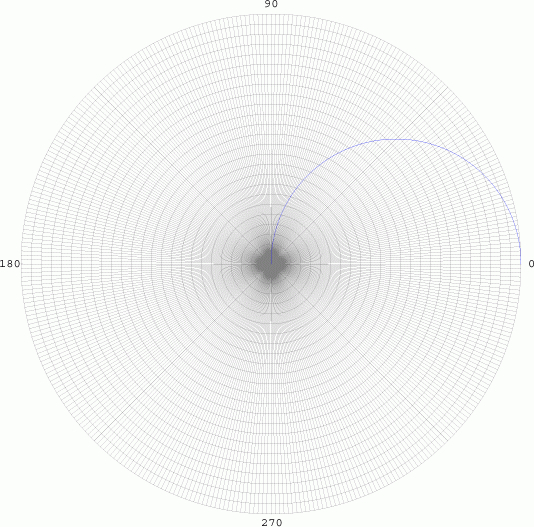
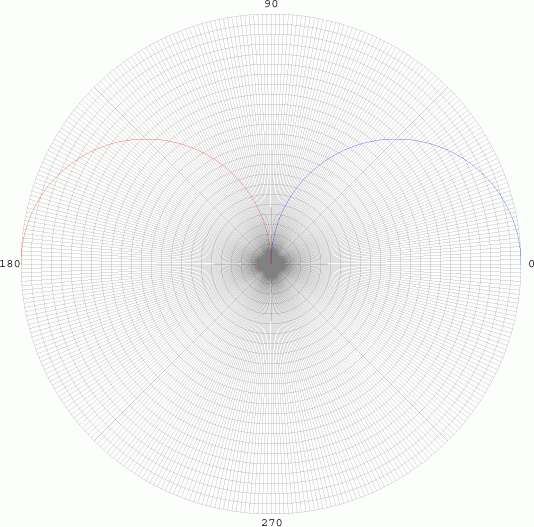
From 0 to 90
degrees, the radius is positive, so the curve is drawn as blue (Top
Left). As the curve goes between 90 and 180 degrees, the radius becomes
negative, and is graphed in red. While this has no significant realistic
interpretations, it does have
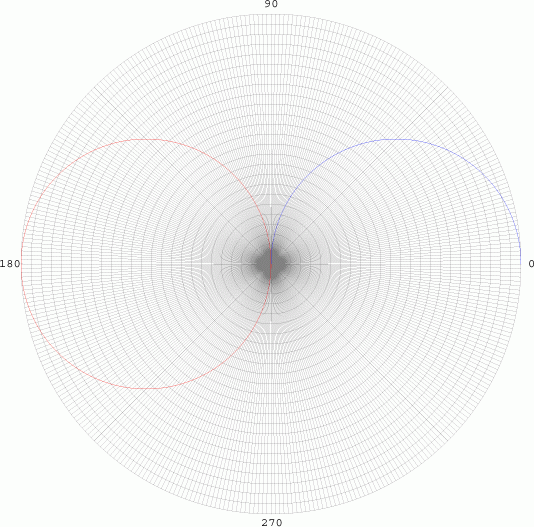
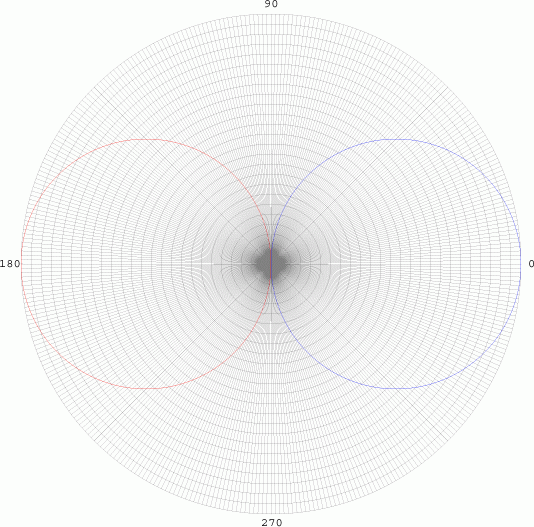

Since there is
no dependency on Φ, the graph is sketched as a pair of tangential
spheres. However, when we evaluate probabilities, we often are square
integrating the function, so we have to take the square of function (in
the case, the square of the radius).
Introduction
Introduction to Quantum Chemistry
Periodic Table
MO Theory
References






