Construction of a Pentagon on the cube Proof of Part I: Pentagon is Equilateral Proof of Part II: Pentagon is in One Plane Proof of Part III: Pentagon is Equiangular Proof of Part IV: Side of Dodec Form Apotome Construction of the Dodecahedron

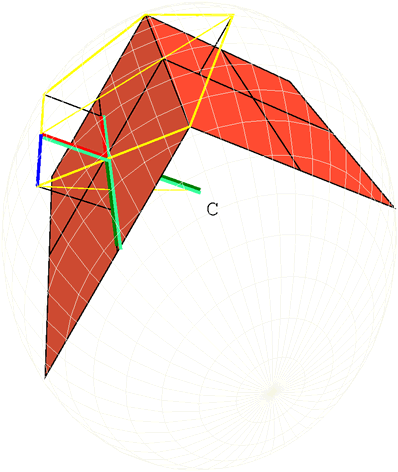
But the square on the radius of the sphere which comprehends the cube is also triple the square on the half of the side of the cube, for it has previously been shown how to construct a cube and comprehend it in a sphere, and to prove that the square on the diameter of the sphere is triple the square on the side of the cube. Euclid XIII.15 But, if the whole is so related to the whole as the half to the half also, and the green line is half of the side of the cube, therefore the thin yellow line equals the radius of the sphere which comprehends the cube. And the intersect point is the center of the sphere which comprehends the cube, therefore the edges on the pentagon are on the surface of the sphere. Similarly, we can prove that each of the remaining angles of the dodecahedron is also on the surface of the sphere, therefore the dodecahedron has been comprehended in the given sphere.

Back To Main Page