 |
||
 |
||
|
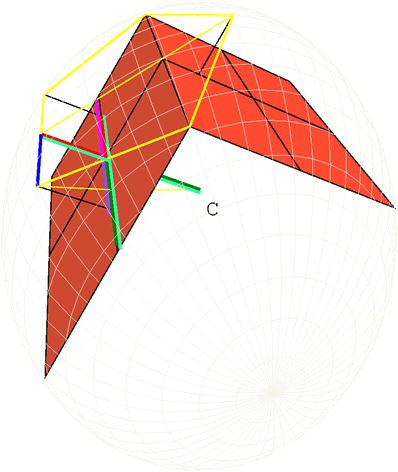
Next we will prove that the side of the dodecahedron is the irrational straight line called apotome. Since, when the horizontal light green line is cut in extreme and mean ratio, the green line is the greater segment, and the red line is the greater segment of the magenta line, Looking at the lines that resides on the left square: Therefore, when the whole line( green line + magenta line) is cut into extreme and mean ratio, the red line + the dark purple line is the greater segment. Thus, green:dark purple = dark purple:(green - dark purple) The same is true of the doubles also, for parts have the same ratio as their equimultiples, therefore (green + magenta) : (red + dark purple) = (red + dark purple):((green - dark purple)+(magenta - red)) Since (green + magenta) > (red + dark purple), then (red + dark purple) > ((green - dark purple)+(magenta - red)) Therefore (green + magenta) is cut in extreme and mean ratio, and (red + dark purple) is its greater But (red + dark purple) = ( blue + yellow), therefore, when (green + magenta) is cut in extreme and mean ratio, (blue + yellow) is the greater segment. And, since the diameter of the sphere is rational, and the square on it is triple the square on the side of the cube, therefore NO, being a side of the cube, is rational. But if a rational line is cut in extreme and mean ratio, each of the segments is an irrational apotome. Therefore UV, being a side of the dodecahedron, is an irrational apotome. |
||
|
||
| Back To Main Page |

