In the same way that the Law of Reflection is the basic tool we use to develop the theory of mirrors, Snell's Law is the basic tool that we use to develop the theory of lenses. In this section, we will discuss single refraction for a circular boundary, where a beam of light passes from one medium into another. The material in this section will then be extended in the next, where we will cogitate on a beam of light that is refracted twice. In other words, we shall be undertaking a study of lenses.

Throughout this section, we will assume that we are travelling from a region of smaller index of refraction to a region with a higher one, so that total internal reflection is not a possibility.

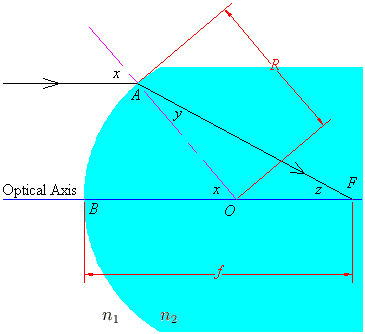
Consider a convex circular boundary (of radius R and center of curvature O) between two regions.

If rays coming in from infinity are close to the optical axis, then we will be dealing with small angles, and the small angle approximation sin(w) = w will be good. We assume that the angles x, y, z as labelled above are small enough so the approximation holds, and we now proceed to find the focus of this setup.

When the ray hits the point A, it refracts according to Snell's Law; using small angle approximations, this reduces to n₁x = n₂y. Also, the angle sum theorems for lines and triangles yield z = x - y.

Using radian measure, AB = Rx, and the relationship AB = fz = f(x - y) holds approximately. Hence, keeping in mind our simplified Snell's Law, we have

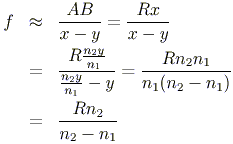
The same equation holds for a concave boundary; for brevity's sake we shall omit the proof. In this case, the focus is the spot from which the refracted rays seem to diverge.

In discussing refraction, we can use the same ray tracing techniques that we used for mirrors. Here, we consider a ray that is bent to intersect the focus, and a ray through the centre of curvature (which is therefore not bent).

Observe the following convex boundary.

We see that the image is inverted and shrunken, and that it is located in the second region.

As with concave mirrors, concave refractive boundaries have three cases.

When the source is beyond the focus, we get a diminished, upright image in front of the source, located between the focus and the centre of curvature.

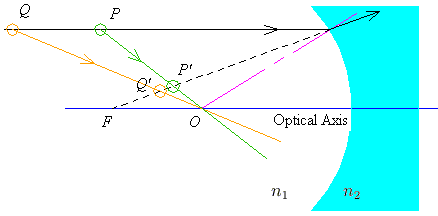
The image must be between the focus and the centre because we are travelling from an area of low index to one with a high index; the refracted ray cannot be bent past the normal line.

When the source is between the focus and the centre of curvature, the image is again diminished and upright.

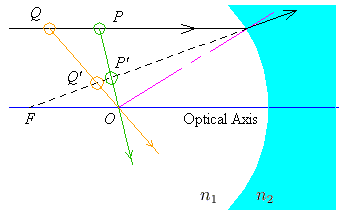
The image must be located between the focus and the centre, and in front of the source.

Finally, the source could be located between the centre and the boundary. In this case, the image is shrunken and upright.

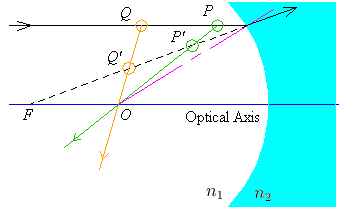
The image will be located between the boundary and the centre; it will also be behind the source. This is an easy consequence of the geometry; since the source is in front of the centre, the ray that goes through the centre must go backwards to intersect the line that goes through the focus.

The image below provides a method for finding the image of an object after refraction at a convex boundary.

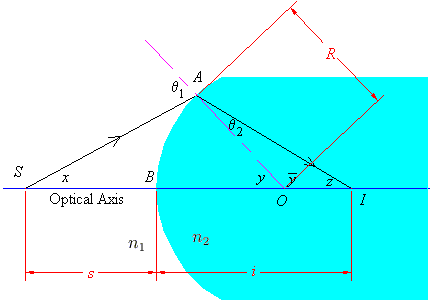
The source is located at S, and the image will be located at I. The centre of curvature is at O, and the radius is R. The angle x can presumably be measured, and the angles of incidence and refraction are related using our small angle approximation of Snell's Law. Using the angle sum theorems for lines and triangles, and radian measure, we find that

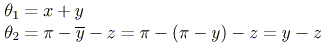
so that our small angle Snell's Law is given by

Using radians, the arclength AB = Ry. For small angles, AB = sx = iz holds. Substituting these formulas into our Snellian approximation gives

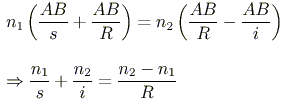
In fact, the equation holds for concave boundaries as well, provided we use sign conventions for our measurements s, i, R.

In our presentation of mirrors, we spoke of sign conventions for measurements that allowed us to use the same formulas for all spherical mirrors. A modified version of these conventions actually allows us to deal with both reflecting and refracting surfaces in a general manner.

Let Side A of an optical component be the side from which light starts, and let Side B be the side to which light travels. With mirrors, Sides A and B are identical. If s is the source distance, i is the image distance, R is the radius of curvature, and f is the focal length, then, our sign conventions are as follows.

• The sign of s is determined by Side A. If the source is on Side A, s is positive; if it is on the side opposite to Side A, s is negative.
• The signs of i, R, f are determined by Side B. For the image and the focal point, their measurements are positive if they are on Side B, and negative if they are on the side opposite to Side B. R is positive provided the centre of curvature is on Side B; it will be negative if it is on the side opposite Side B.

It cannot be stressed enough that for a mirror, Sides A and B are the same.