The parametrization of Pythagorean triples

If a, b, and c are all positive integers, this is called a Pythagorean triple. The best known example, and the simplest one, is 3, 4, 5 since

and another well known one is 5, 12, 13.

How can we find all Pythagorean triples?

If a, b, c is a Pythagorean triple, then so is ma, mb, mc for any positive integer m. Thus in order to find all of them, it suffices to find those which are primitive - i.e. for which there does not exist a common divisor of all three coordinates.

• If a,b,c is a Pythagorean triple, then it is primitive if and only if ts coordinates are pair-wise relatively prime.

Because if a prime number p divides two of them, say a and b, it will also divide c², hence c.

If a and b are both even, then a²+b² will be even as well, and they cannot be part of a primitive Pythagorean triple. If a and b are both odd, then a²+b² will be congruent to 2 modulo 4, and it cannot be the square of an integer. Therefore in a primitive Pythagorean triple exactly one of a and b is odd and one even.

If (a, b, c) is a primitive Pythagorean triple, then the point (a/c, b/c) is a point on the unit circle with rational coordinates expressed as reduced fractions. In fact, finding all Pythagorean triples turns out to be nearly equivalent to finding all such points.

How can we find all points (A, B) on the unit circle with rational coordinates?

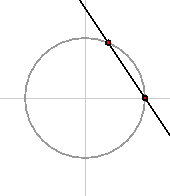
If (A, B) is a rational point on the unit circle other than (1,0), then the line through (A,B) and (1,0) has the equation

whose slope is the rational number m = B/(A-1). Conversely, if m is any rational number then the line through (1,0) with slope m intersects the unit circle at one other point. Thus there is exactly one rational point on the unit circle for each rational slope. Those with positive coordinates correspond to slopes m less than -1.

Rational points on the circle and primitive Pythagorean triples

and if exactly one of p, q is even and one odd then the triple

will be a primitive Pythagorean triple. Conversely, suppose that a, b, c be a primitive Pythagorean triple. One of a, b is even - say b = 2n. Then

Since c and a are relatively prime, so are the factors (c-a)/2 and (c+a)/2, so that each of these is also a square. Set

which implies that b = 2pq.

References

• O. Neugebauer, The exact sciences in antiquity, Dover, 1969. This is a reprint of the 1957 second edition. In Chapter 2 is a discussion of how the Babylonians might have come across the parametrization we have described.

Written by Bill Casselman.