
[ An image at higher resolution ]

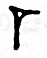 and the numbers 2 through 9 were written by combining multiples
of a single stroke:
and the numbers 2 through 9 were written by combining multiples
of a single stroke:

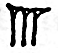
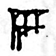
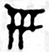
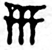
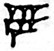


The number 10 was written in a single character
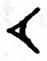 and the
numbers 20 to 50 were written with multiples of this character:
and the
numbers 20 to 50 were written with multiples of this character:




The numbers up to 59 were obtained by combining these much as we
do. For example, 11 was written as  .
But the system was not actually based on 10, but rather on 60 -
and it was a true floating point system so that 1 and 60
(as well as, say, 3600) were indistiguishable.
All numbers could be obtained by combining these in order,
writing from left to right as we do. Thus seventy was written
as
.
But the system was not actually based on 10, but rather on 60 -
and it was a true floating point system so that 1 and 60
(as well as, say, 3600) were indistiguishable.
All numbers could be obtained by combining these in order,
writing from left to right as we do. Thus seventy was written
as  .
Sometime before 300 BCE, but after Plimpton 322 was written,
a special symbol was devised as a zero, but in Plimpton 322
there is potential confusion because of this problem.
The conventional way to write floating point sexagesimal numbers is
by using comma separators, so that 1,29 is 60+29 = 89 in decimal notation,
and 1,1,1 is 3661.
.
Sometime before 300 BCE, but after Plimpton 322 was written,
a special symbol was devised as a zero, but in Plimpton 322
there is potential confusion because of this problem.
The conventional way to write floating point sexagesimal numbers is
by using comma separators, so that 1,29 is 60+29 = 89 in decimal notation,
and 1,1,1 is 3661.
The last two columns. At any rate, we now know almost enough to read the right hand columns of the tablet. The last column (with a few natural interpolations to take into account missing symbols for 5, 6, and 15, ) simply numbers the line of numerical data. In the fourth column is written the word pronounced ki which can be translated loosely here as number, so that the fourth and fifth column together (number 1, number 2, etc.) just enumerate the different lines of data. Interpolations are in green.

For the rest of the columns, we show in order the original column, the sexagesimal numbers written in conventional notation, and then the decimal equivalents. Error corrections are in red. Both interpolations and corrections are explained later on. All the zeroes are interpolated, also, since the Babylonians at this time did not have them.
Column two. The heading of the second column includes the word for width.


Column three. The heading of the third column includes the word for diagonal.


Column one. The heading of the first column has not been translated. We shall see in a moment the reasons for placing the `decimal point'.


which form the sides of right triangles. Here is the resulting table of calculations, in modern notation (with discrepancies in square brackets):
A bit later, we shall confirm this theory by explaining the errors.
As for the first column, it contains the values of d2 / l2 . For example, in the first row d = 169, l = 120, and d2/l2 = 1.9834 ... = 1,59,0,15.
Here are the values of p, q, and m for the triples in the table:
The ratio c/b is equal to (p2 + q2)/2pq = (1/2)(p/q + q/p). Therefore this ratio, the square of which appears in the first column of the tablet, will have a finite expression in base 60 if 1/p and 1/q do. The Babylonians almost certainly understood the difference between finite sexagesimal expansions and repeating ones, and in particular we have found tables of reciprocals 1/p for many values of p where the expansion is finite. Such numbers p are called regular by Neugebauer. It is not likely to be a coincidence that the values of both p and q associated to the rows of the tablet are regular, and in fact that in all but one case the expansions of 1/p and 1/q appear in the tables of reciprocals that have been found. It seems plausible, therefore, that the Babylonians knew how to generate primitive Pythagorean triples.
We know something, therefore, about how the tablet was constructed, but we do not know exactly why it was constructed. The ordering of the rows according to the size of the first column suggests that it might have been used in an early form of trigonometry. Perhaps it was constructed from Pythagorean triples just to make arithmetic easier.
However incomplete our present knowledge of Babylonian mathematics may be, so much is establshed beyond any doubt: we are dealing with a level of mathematical development which can in many aspects be compared with the mathematics, say, of the early Renaissance. (O. Neugebauer in The exact sciences in antiquity)
As confirmation of both the interpretation of the table and this conjecture regarding p and q, the four apparent errors can be reasonably explained:
Written by Bill Casselman.