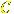|
It is possible to develop the subject of Coxeter groups entirely
in combinatorial terms (this is done - well, at least thoroughly attempted - in
the book by Bourbaki), but certain geometric representations
of Coxeter groups, in which the group acts discretely
on a certain domain, and in which the generators are
represented by reflections, allow one to visualize nicely
what is going on.
Recall that a linear reflection is a linear transformation
fixing a hyperplane passing through the origin and acting
as multiplication by -1 on a line through the origin transverse to this hyperplane.
There are other kinds of reflections, too, but they reduce to
linear ones. They are discussed at the end of this section.
Single reflections
If s is a reflection in a space V,
there exists a linear functional a and
a vector av
so that the reflection takes v to
v - < a, v > av.
The hyperplane fixed by the reflection is where a = 0,
and av is mapped to its negative as long as < a , av > = 2.
The function a and vector av
are unique up to non-zero scalar multiples.
If a is replaced by
ca then av is replaced by c-1av.
Often a reflection will be orthogonal with respect to
some inner product  , when the reflection takes v to , when the reflection takes v to
v - 2 (av  v) / (av v) / (av  av) . av) .
In this situation, the dot product induces
a linear map from V to the linear dual space V*, and a is the image of
2 av / (av  av). av).
The group GL(V) acts by its definition on V,
and on V* according to
the prescription < ga, gv > = < a, v >.
(If vectors are column vectors, then linear functions are row vectors
and the canonical pairing is the matrix product a v.
If g is represented by the matrix M then g takes
v to Mv and a to a M-1.)
At any rate, the group GL(V) acts transitively on pairs (a, av),
hence all reflections are conjugate to each other.
Pairs of reflections
Suppose s and t to be a pair of reflections.
Such pairs turn out to make up essentially
a one-parameter family of conjugacy classes.
Let s and t be a pair of reflections, say corresponding to
a, av and b, bv.
Define associated real constants
|
|
cs, t = < a, bv >
ct, s = < b, av > .
|
Let (s1, t1) and (s2, t2) be pairs of reflections, conjugate
under the linear transformation g. Then
|
|
ga1 = ca a2
ga1v = ca-1 a2v
gb1 = cb b2
gb1v = cb-1 b2v
|
for some non-zero constants ca and cb, and
consequently cs2, t2 = (cb/ca) cs1, t1,
ct2, s2 = (ca/cb) ct1, s1.
The constants cs, t and ct, s are therefore not
conjugation-invariant,
but the product ns,t = cs, tct, s is.
For generic pairs it will turn out to possess a simple interpretation.
One way to understand conjugation-invariant phenomena
is to consider geometrical configurations - for example,
how the various hyperplanes and lines relate qualititatively to each other.
One possibility is that in which
the reflection hyperplanes of s and t are the same.
In this case we may take a = b. Then
|
|
cs, t = < a, bv > = < b, bv > = 2
ct, s = < b, av > = < a, av > = 2
|
so that ns, t = 4. Similarly ns, t = 4 when av and bv
are linearly dependent.
Proposition 2. When ns, t is not equal to 4,
then a and b are linearly independent, as are av and bv.
The plane spanned by av and bv is transverse to
the linear subspace of codimension 2 where a and b are both equal to 0.
Proof. Only the last claim remains to be proven.
Exercise 8.
Verify the last claim.
We are especially interested in the case where ns, t = 4 but
a and b are linearly independent.
If L is the intersection of the kernels of
a and b, then s and t induce reflections
on the two-dimensional quotient V / L. In this plane
av and bv are linearly dependent. We have
cs, tct, s = < a, bv > < b, av > = 4,
and we can scale a so that in fact
cs, t = ct, s, both being equal to
2 or -2. In either case, av and bv lie on a single line through
the origin, and both s and t transform a vector v in a direction parallel to that line.
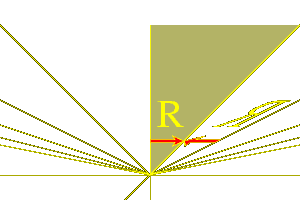
In particular the products st and ts are shears along that line.
|
|
|
s
|
t
|
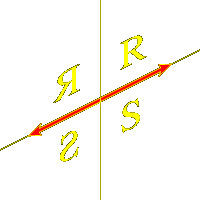
The region on one side of that line and in between the two lines
a=0 and b=0 will be a fundamental domain for the group acting
on the corresponding open half-plane.
If we choose the signs of a and b correctly we may assume that
this region is that where a > 0 and b > 0. In that case, with our normalization,
cs , t = ct, s = -2.
Exercise 9.
In the situation described above,
explain how s and t act on the space V* dual to V.
This is of importance in the theory of Kac-Moody Lie algebras,
since V* contains the roots of the algebra.
Exercise 10.
Show that in dimension 2 there are three
conjugacy classes of pairs (s, t) with ns, t = 4 and in dimensions
greater than 2 there are four.
From now on, suppose that ns, t is not equal to 4.
Then the vectors av and bv span a plane transversal
to the intersection of the kernels of a and b, and in effect we
may restrict ourselves to dimension 2. In these circumstances,
reflections fix lines.
There is one other exceptional collection of cases
to deal with - when ns, t = 0. This happens only when either
cs, t = < a, bv > = 0 or ct, s = < b, av > = 0. If both are equal to
0, then s and t are a commuting pair of reflections whose product
amounts to multiplication by -1. The group generated by s and t
has four elements, and any one of the four quadrants is a fundamental
domain.
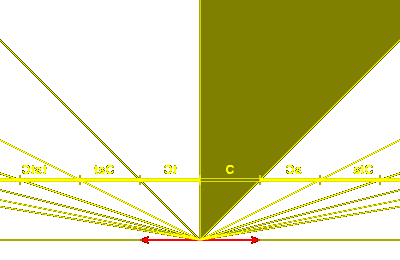
Otherwise, suppose that < a, bv > = 0,
but < b, av > is not equal to 0.
We may arrange that < b, av >
is in fact positive.
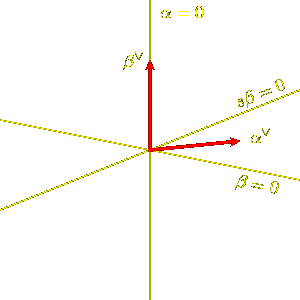
Then the line a = 0 is fixed by both s and t.
The reflection s interchanges the two sides of this line, but t
preserves it.
The pair of reflections t and sts
now both stabilize each side of the line a = 0, and the n-invariant
of this pair is 4, since they share the eigenvector bv.
Therefore from what have already learned in this case,
we know that with a suitable choice of sign for b
the region C where b > 0 and sb > 0 on the side
of the line where a > 0 is a fundamental domain
for the group generated by t and sts. Furthermore,
the reflection s takes C to -C. Note also
that the vector av lies in its interior, as shown in the figure.
Later on we shall need a simple consequence of this
clear picture of how the pair s and t act:
in this case the region where a > 0, b > 0 is not
a fundamental domain for the group generated by s
and t. Or, in other words, if ns, t = 0 and this region is
a fundamental domain then s and t are
a commuting pair of reflections, and cs, t and ct, s both vanish.
From now on, we assume ns, t to be neither 0 nor 4.
Proposition 3. If n be neither 0 nor 4,
there is a unique conjugacy class of pairs (s, t) of reflections with ns, t = n.
Proof. Let s be any reflection, say corresponding to a, av.
All choices of s are certainly conjugate.
We may as well take a to be the function x
and the vector av to be (1, 0). The matrices commuting
with s are then the diagonal matrices. We now look for b and bv with
< b, bv > = 2, < a, bv > < b, av > = n.
Let b be any linear function independent of a
and not vanishing on av. All choices are
conjugate by a linear transformation preserving a and av.
Suppose c = < b, av >.
It remains to choose bv independent of av
with < a, bv > = n/c. This requires that n differ from 4,
and then all choices are conjugate by a linear transformation fixing both the line
a = 0 and that through av.
Proposition 4. Take av and bv as a basis of V. The matrices of
s, t, and st are then
As one consequence, -2 + ns,t is the trace of st,
hence clearly conjugation-invariant.
Proposition 5.
Suppose ns, t to be neither 0 nor 4. Then there exists
a non-degenerate quadratic form invariant under both
s and t, unique up to scalar multiple. It will be definite
if and only if 0 < ns, t < 4.
Proof.
Suppose that u  v is an inner product invariant under
s and t. This happens if and only
if av is perpendicular to the line
a = 0, and similarly for bv and b.
The space of vectors fixed by s is spanned by
cs, t av - 2bv, and that fixed by t is
spanned by 2av - ct, s bv. For invariance,
therefore, we must have v is an inner product invariant under
s and t. This happens if and only
if av is perpendicular to the line
a = 0, and similarly for bv and b.
The space of vectors fixed by s is spanned by
cs, t av - 2bv, and that fixed by t is
spanned by 2av - ct, s bv. For invariance,
therefore, we must have
(cs, t av - 2bv)  av = 0 av = 0
(2av - ct, s bv)  bv = 0 bv = 0
cs, t (av  av) - 2 (bv av) - 2 (bv  av) = 0 av) = 0
cs, t (av  av) = 2 (bv av) = 2 (bv  av) av)
2 (av  bv) - ct, s (bv bv) - ct, s (bv  bv) = 0 bv) = 0
ct, s (bv  bv) = 2 (av bv) = 2 (av  bv) bv)
|
Since ns, t is not 0, neither cs, t nor ct, s vanish.
Therefore the single number av  bv determines
the inner product on all of V. bv determines
the inner product on all of V.
The matrix of the quadratic form is
In order for the form to be definite, it is necessary
and sufficient that cs, t and ct, s have
the same sign, and that the determinant be positive.
Therefore we must have 0 < ns, t < 4. QED
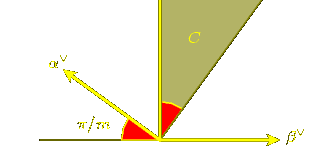
Proposition 6.
In order for the group generated by s and t to be finite,
it is necessary that one of these hold:
-
s = t (when n = 4);
-
s and t commute (when n = 0);
-
n = 4 cos2
 p / m for some positive integers m and p < m. p / m for some positive integers m and p < m.
In the last case, the region a > 0 and b > 0 will be a fundamental
domain for the group precisely when p = 1, and cs, t and ct, s are both negative.
The picture accompanying the last assertion is this:
Exercise 11.
Prove this in detail.
Suppose now that n is not 4, and that
s and t generate an infinite group.
We want again to see when the region a > 0, b > 0 is
a fundamental domain. From one of the Propositions just proven,
we must have n > 4 or n < 0.
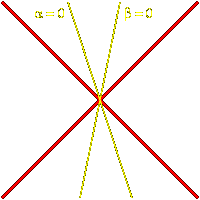
Proposition 7.
The elements s and t generate an infinite group
with fundamental domain a > 0, b > 0 if and only if
n is greater than or equal to 4,
and both cs, t and ct, s are negative.
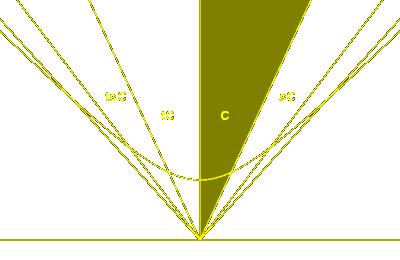
Proof. The case n = 4 has been dealt with. It remains to show
that n cannot be negative. This case can be eliminated by
using the invariance of the pair of lines where the indefinite metric
vanishes. The following images portray what things look like (the
red lines are where the invariant indefinite quadratic form vanishes):
|
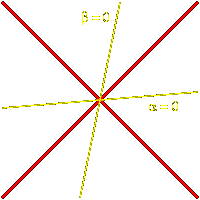
|
|
n > 4
|
n < 0
|
Exercise 12.
Finish the proof. (Hint: the reflection s preserves the
`cones' through which a = 0 passes. What does it do
to the other two? This situation is somewhat like the one we saw where n = 0.)
In summary:
Theorem 8.
Assume that s and t are a pair of reflections in space
with reflection data a, av and b, bv. Assume also
that the region a > 0, b > 0 is a fundamental domain for the group
they generate. Exactly one of the following cases occurs:
- s and t commute, and cs, t = ct, s = 0;
- st has finite order m > 2,
and ns, t = 4 cos2
 /m; /m;
- st has infinite order
and n
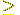 4. 4.
In the last two cases, cs, t and ct, s are both negative.
Affine reflections
An affine reflection
reflects points in an affine hyperplane f(x) = 0
for some affine function f(x).
The function f can be expressed as
f(x) = < a, x > + c
for some linear function a and constant c. The linear function a
is the gradient of f, and for any point x in V
and vector v we have f(x + v) = f(x) + < a, v >.
The reflection then takes a point x to x - f(x) av for some vector av in V
with < a, av > = 2.
An affine reflection is a special case of a linear one, through
the familiar trick of embedding an affine space of dimension
n into a vector space of dimension n+1. Thus v in V
maps to (v, 1) in a larger space V#.
Let 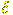 be the function on V# taking (v, x) to x.
The affine reflection on V corresponding to a, av, and c
is the restriction to V
of the reflection defined by the linear function a + c be the function on V# taking (v, x) to x.
The affine reflection on V corresponding to a, av, and c
is the restriction to V
of the reflection defined by the linear function a + c 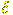 on U.
In the discussion of pairs of reflections
with n = 4 we have already seen an implicit example of this. on U.
In the discussion of pairs of reflections
with n = 4 we have already seen an implicit example of this.
Non-Euclidean reflections
A non-Euclidean reflection reflects points of a non-Euclidean
space in a non-Euclidean hyperplane. This also can be explained in terms of
linear reflections.
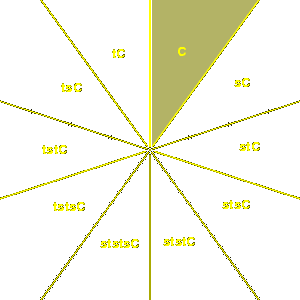
The non-Euclidean space Hn of n dimension is the component
Q(x) = xn+12 - x12 - ... - xn2 = 1, xn+1 > 0 of
the hyperbolic sphere,
which can be parametrized by Euclidean space En according to the formula
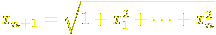
It is taken into
itself by the connected component of the orthogonal group of Q
and there is a unique Riemannian metric on it invariant
under this group and restricting to the Euclidean metric
at (0, 0, ... , 0, 1). There are two models of this
in Euclidean space of n dimensions,
the familiar Poincaré model and the slightly less familiar Klein model.
(There is also, for n=2, the upper half-plane, but that is another
story.)
Both models identify H with the interior of the unit ball
in En centred at the origin.
For the Klein model, this ball
is identified with the intersection of the slice
xn+1 = 1 of the region Q(x) > 0
(the interior of a homogeneous cone). A point x on H maps to
x* = x/xn+1. It happens that a non-Euclidean geodesic line
between two points x and y is the intersection with
H of the plane through the origin
containing x and y, and this intersects the slice in a line
between x* and y*. Thus in the Klein model.
points of H are identified with points of the interior
of a unit ball, and geodesics between such points are line segments in the ball.
The Poincaré model is a transformation of the Klein model.
A point x in the interior of the unit ball in En
maps to the point above it on the upper hemisphere in En+1,
then by South pole stereographic projection back onto the equator.
In this transformation, geodesics become arcs of circles
perpendicular to the boundary of the unit ball.
The point for us is that non-Euclidean reflections
are those induced on the hyperbolic
sphere, or either of its models, by linear reflections in En+1.
For both models, we start with a hyperplane a = 0 which intersects the
region Q(x) > 0 and a vector av transverse to it. In the Klein model,
we take a point x in the slice Q(x) > 0, xn+1 = 1 to
x - < a, x > av and then project it back onto the slice.
We have seen examples of this also in the discussion above of pairs
of linear reflections with n > 4.
In the Poincaré model we unravel by stereographic projection, reflect, and ravel again.
Exercise 13.
Design an algorithm to draw the geodesic between two points
of the unit disc in the Poincaré model. There are two ways to approach this
problem, depending on the tools available for drawing. (1) Suppose all you can do
is produce line segments and circles, then you must first decide whether to
draw a line or a circle; if it is a circle, you must find the centre,
radius, and arc. This becomes delicate only for
points nearly lying on a diameter of the unit disc, and suffers to
some extent from stability. Discuss how serious this is, analyzing
how continuously your drawing depends on the two points. (2) if you
can draw Bezier curves, then you should probably use them to approximate circles.
Use one or two bisections to allow a reasonable approximation;
then use velocity vectors to find the control points. The best way to do
all this is likely through stereographic projection, since the geodesics in the disc
correspond to simple latitude circles on the sphere.
|
In this section we shall look at some Coxeter groups defined geometrically.
Finite dihedral groups
Suppose P to be a regular polygon in the plane. That is to
say, it is a polygon of m sides for some m > 2, centred at the origin,
and invariant under rotations by 2  / m. / m.
Rotations are not its only symmetries,
since any line through the center of any of its sides
and the origin, or any of its corners and the origin,
is an axis of mirror symmetry. Since any symmetry must take
a corner into some other corner, and can either preserve
or reverse orientation, there are 2m symmetries altogether,
in which the rotations form a subgroup of order 2.
Proposition 9. The symmetry group of
a regular polygon of m sides is a Coxeter group
with two generators, say s and t. We have ms, t = m.
This should be clear from the picture. The generators s and t
should be chosen to be reflections in neighbouring axes of symmetry,
as the red lines in the figure.
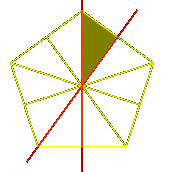
They are orthogonal reflections, with the angle between their
lines of reflection equal to  /m. Choosing the signs
of av and bv correctly, we have av /m. Choosing the signs
of av and bv correctly, we have av  bv = -2 cos ( bv = -2 cos ( /m).
The region where a > 0 and b > 0 is a fundamental domain
C for the symmetry group. /m).
The region where a > 0 and b > 0 is a fundamental domain
C for the symmetry group.
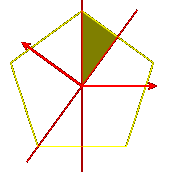
The 2m elements of the group can be expressed as
1, s, t, st, ts, ... , st ... = ts ... (m terms)
We can see how these elements match up with transforms of C in this
picture:
Affine dihedral groups
Now we look at the group generated by affine reflections in the
points at the end of a line segment in one dimension.
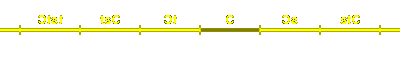
It is an infinite Coxeter group with two generators, say s and t,
and with ms, t infinite.
As we have already seen, the realization by affine reflections
is the restriction to a line of
a linear Coxeter group in dimension 2.
Again, if a and b are chosen correctly, the region where
a > 0 and b > 0 is a fundamental domain for the group.
The elements of the group can be expressed as
1, s, t, st, ts, sts, tst, ...
Hyperbolic dihedral groups
Now we look at the group generated by two hyperbolic reflections
in the ends of a segment on the hyperbola Q(x, y) = 1,
where Q is an indefinite non-degenerate quadratic form.
It, too, is an infinite Coxeter group with two generators.
And again, if a and b are chosen correctly, the region where
a > 0 and b > 0 is a fundamental domain for the group.
An observation about groups of rank two
The examples we have just examined exhaust the possible
representations of rank two Coxeter groups
with the property that the region C where
a > 0, b > 0 is a fundamental
domain.
An observation we shall need later, based on
observation of these cases, is that
Proposition 10. In these circumstances,
if s is a generator in S then
sw > w if and only if C and wC lie on the same side of
the line as = 0.
.
In brief, the argument for this is that if sw > w
then w = ts .. , and the shortest gallery
(sequence of contiguous chambers) from C to swC through chambers
is the reflection of the one from C to wC, except that
it starts with an extra transition from C to sC.
To be more explicit, the shortest gallery from C to wC is
the sequence
C, tC, stC, ... and is reflected into the longer
gallery C, sC, stC, stsC, ...
Groups of rank 3
Suppose now that s0, s1, and s2 generate
a Coxeter group W of rank 3 with Coxeter matrix
(mi, j) for i, j = 1, 2, 3.
I assume that all the mi, j are finite,
so that all
the dihedral groups Wi, j are finite.
How can we tell whether W is finite?
We know that the standard
representation preserves a metric in which
|ai|2 = 1 for all i and ai  aj = -cos ( aj = -cos ( /mi, j)
for i distinct from j. If we assume that
the indexing is chosen so that m1, 2 differs from 2,
then by choosing coordinates suitably (so that the finite Coxeter
group generated by the first two reflections stabilizes the (x, y)-plane)
we can arrange this metric to be x2 + y2 + c z2
with c = 1, 0, or -1, and a1 = (1, 0, 0),
a2 = (-cos /mi, j)
for i distinct from j. If we assume that
the indexing is chosen so that m1, 2 differs from 2,
then by choosing coordinates suitably (so that the finite Coxeter
group generated by the first two reflections stabilizes the (x, y)-plane)
we can arrange this metric to be x2 + y2 + c z2
with c = 1, 0, or -1, and a1 = (1, 0, 0),
a2 = (-cos  /m1,2, sin /m1,2, sin  /m1,2, 0). In order to
find a3 we have to take into account the conditions /m1,2, 0). In order to
find a3 we have to take into account the conditions
- |a3|2 = 1
- a3
 a1 = - cos a1 = - cos  /m1, 3 /m1, 3
- a3
 a2 = - cos a2 = - cos  /m2, 3 /m2, 3
We may assume that a3 = (x, y, z) with z > 0.
So these equations become
- x2 + y2 + c x32 = 1
- (x, y, z)
 (1, 0, 0) = - cos (1, 0, 0) = - cos  /m1,3 /m1,3
- (x, y, z)
 (-cos (-cos  /m1, 2, sin /m1, 2, sin  /m1, 2, 0) = - cos /m1, 2, 0) = - cos  /m2, 3 /m2, 3
or
- x = - cos
 /m1,3 /m1,3
- cos
 /m1, 3 cos /m1, 3 cos  /m1, 2 + y sin /m1, 2 + y sin  /m1,2 = - cos /m1,2 = - cos  /m2, 3 /m2, 3
- cz2 = 1 - x2 - y2
Proposition 11.
Let r = 1 - 1/m1, 2 + 1/m1, 3 + 1/m2, 3.
Then
- if r < 0 then c > 0 and W is finite;
- if r = 0 then c = 0 and W stabilizes a half-plane, and it acts by affine
reflections on a plane parallel to its boundary;
- if r > 0 then c < 0 and the group acts by non-Euclidean reflections.
Proof. It all depends on how  - -  /m2, 3 compares to /m2, 3 compares to
 /m1, 2 + /m1, 2 +  /m1, 3. For example, if they are equal, then
the cosine sum formula allows us to set y = sin /m1, 3. For example, if they are equal, then
the cosine sum formula allows us to set y = sin  /m1, 3.
This gives us x2 + y2 = 1,
c = 0, z arbitrary. The group preserves the whole (x, y) plane.
Etc. /m1, 3.
This gives us x2 + y2 = 1,
c = 0, z arbitrary. The group preserves the whole (x, y) plane.
Etc.
Here is a table of cases of possible values of the mi, j
in weakly increasing order:
| Finite: |
2, 3, 3; |
2, 3, 4; |
2, 3, 5; |
| Affine: |
3, 3, 3; |
2, 4, 4; |
2, 3, 6; |
The regular solids
The classification of the finite Coxeter groups in three
dimensions is intimately related to
the classification of the regular solids.
Exercise 14.
Verify that the Coxeter subgroup with values of m
equal to 2, 3, 3 is the symmetry group of the regular
tetrahedron.
Exercise 15.
Verify that the Coxeter subgroup with values of m
equal to 2, 3, 4 is the symmetry group of the
cube and the regular octahedron.
2, 3, 4
Exercise 16.
Verify that the Coxeter subgroup with values of m
equal to 2, 3, 5 is the symmetry group of the icosahedron
and the dodecahedron.
Exercise 17.
Prove directly that the symmetry group of any
regular polyhedron is a Coxeter group.
Exercise 18.
Verify that the symmetry group of the regular simplex in
n dimensions is a Coxeter group.
Exercise 19.
Verify that the symmetry group of the cube in
n dimensions is a Coxeter group.
Affine Coxeter groups of rank 3

|
|
Affine A2
|
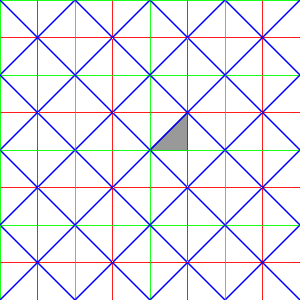
|
|
Affine B2
|
|
|
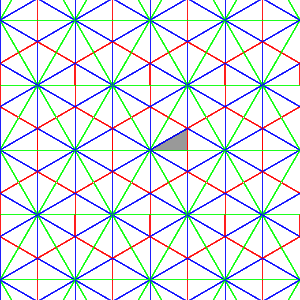
Affine G2
|
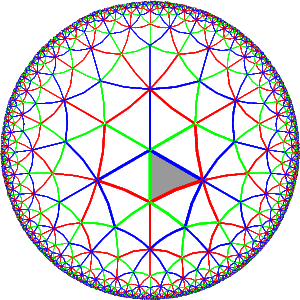
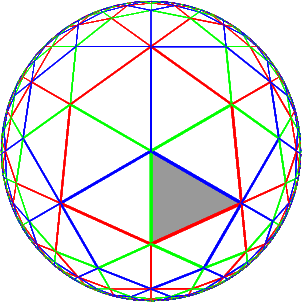
A hyperbolic Coxeter group of rank 3
|
|
Poincaré model
|
|
|
Klein model
|
|
|
A polyhedral realization of a Coxeter group
is a linear representation in which
- The group possesses a fundamental domain C
which is a polyhedral cone;
- the generators in S are represented by reflections in the walls of
this cone.
I do not exclude the case where the cone is invariant under translation.
This for a group with a single generator a single hyperplane
is admissible in any dimension.
In these notes, we shall use only
simplicial realizations
where the polyhedral cone is simplicial, its walls
parametrized by S. The dimension of a simplicial realization
must be at least the rank of the group.
Every Coxeter group possesses at least
one realization, as we shall see
in a moment.
Geometric properties of realizations translate naturally to
combinatorial properties of the group. From the geometry
of the simplices neighbouring a fundamental
domain, for example, you can read off the Coxeter matrix.
This is because if L the intersection of two walls, then the configuration
in the neighbourhood of L is
essentially that in a realization of the group
generated by the two reflections in those walls.
This is a special case of a very general result
proven in most generality by MacBeath around 1964.
Given a realization, make a choice for each s in S of a
pair as, asv defining reflection in
the wall of the fundamental domain parametrized by s.
The sign of each function as
can (and always will) be made so that as > 0 in the interior
of the given fundamental domain. Such a linear function as is
determined up to a positive scalar multiple, and its equivalence class
under such multiplications will be called a basic root of the realization
(and implicitly also of the choice of fundamental domain).
The half-space As where as > 0 is determined by this class,
and will be called
a basic geometric root of the realization.
The hyperplane as = 0 will be called a basic root hyperplane.
This terminology is not common, but for
general Coxeter groups this notion of
root is entirely natural, since the particular choice
of as has no intrinsic significance. This is not the case
if the Coxeter group is the Weyl group
of a Kac-Moody Lie algebra,
since in that case the roots themselves
are part of the structure of the Lie algebra.
The Cartan matrix associated to
a choice of functions as is the matrix cs, t = < as, atv >.
If the as are chamnged to dsas then cs, t is cahmnged
to ds cs, t dt-1. This gives rise to a new matrix
DCD-1 where D is a diagonal matrix with
positive entries. But the numbers ns,t = cs, tct, s
depend only on the realization itself. The next result
is a consequence of observations made earlier about
conjugacy classes of pairs of reflections:
Theorem 12. In any realization, the Cartan matrix satisfies these conditions:
- cs, s = 2;
- cs, t = 0 if and only if ct,s = 0;
- cs, t is either 0 or a negative number;
- if ns, t lies between 0 and 4 then
it is equal to 4 cos2 (
 /ms, t). /ms, t).
This theorem is apparently due originally to Vinberg.
A real matrix C satisfying these conditions
for a given Coxeter matrix is called an abstract Cartan
matrix. It determines
a Coxeter matrix in a natural way. The numbers
ns, t will always be non-negative; the finite
values of ms, t are determined by conditions
(2) and (4) for the
values of ns, t lying in [0, 4); and ms, t is
infinite for n which are 4 or larger.
Any Cartan matrix clearly gives rise to a representation
of the associated Coxeter group. In fact:
Theorem 13. The representation of a Coxeter group
determined by any abstract Cartan matrix is a realization of
the associated Coxeter group.
This will be proven in the next section.
One consequence is that every Coxeter group has at least one realization, since there
exists always the standard Cartan matrix
cs,t = -2 cos( /ms,t) . /ms,t) .
Cartan matrices with integral matrices determine
Kac-Moody Lie algebras. In this case the representation
of its Weyl group on the lattice of roots is the one associated to this Cartan matrix.
Coxeter groups which occur as the Weyl groups
of Kac-Moody algebras are called crystallographic,
and are distinguished by the property
that for them the numbers ms, t are either
2, 3, 4, 6 or infinite.
Two Cartan matrices C1 and C2
will give rise to
isomorphic representations of
a Coxeter group
if and only if there exists a positive diagonal
matrix D with C2 = D C1 D-1.
In particular, those Cartan matrices giving rise to realizations equivalent to
the standard one are symmetrizable.
Proposition 14.
If each ms, t is finite, then the isomorphism classes of
Cartan realizations are parametrized by H1( 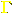 , R)
(where , R)
(where  is the Coxeter diagram). is the Coxeter diagram).
Proof.
If all ms, t are finite, then
all Cartan matrices are of the form
cs, t ds, t where cs, t = -2 cos2 /ms, t
and ds, t is an arbitrary matrix of positive
real numbers with dt, s = 1/ds, t.
Two of these will give isomorphic represntations of W
when the entries differ by factors ds/dt, with all ds > 0.
But the assignment of ds, t to (s, t) defines
a cocycle on the Coxeter graph with values in the multiplicative group
of positive real numbers, and assignments ds/dt are
coboundaries. Conclude by applying the logarithm. /ms, t
and ds, t is an arbitrary matrix of positive
real numbers with dt, s = 1/ds, t.
Two of these will give isomorphic represntations of W
when the entries differ by factors ds/dt, with all ds > 0.
But the assignment of ds, t to (s, t) defines
a cocycle on the Coxeter graph with values in the multiplicative group
of positive real numbers, and assignments ds/dt are
coboundaries. Conclude by applying the logarithm.
Corollary. If W is finite,
then the Coxeter diagram has no circuits.
Proof. Because if the diagram were not a tree, the group would possess
a continuous family of non-isomorphic representations of dimension r.
Distinct classes can give rise
to realizations with very different geometric properties.
We have seen this already in the case of the infinite
dihedral group,
and here are the pictures for two
different realizations of the Coxeter group whose Coxeter
diagram is 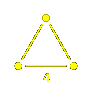 : :

|
|
The Klein model of the standard realization
|
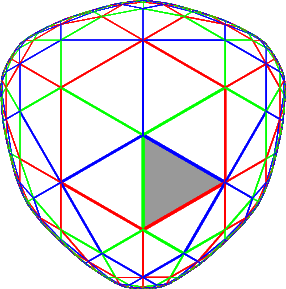
|
|
The Kac-Vinberg realization
|
The first of these is associated to the standard Cartan matrix,
and the second to the integral matrix
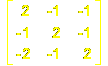
which is that of a certain hyperbolic Kac-Moody Lie algebra.
It is the second, therefore, which is likely to have intrinsic significance.
Exercise 20.
Does the Coxeter group of rank 3 with all ms, t = 3 have
non-equivalent Cartan matrices?
Exercise 21.
(This is a research problem! ) Prove that the boundary
of the second is non-smooth everywhere
(i.e. even though it does have tangent lines everywhere, it
will not likely be C2). (This conjecture is consistent with,
but not directly related to, a curious result of Kac & Vinberg,
which asserts that if the boundary of the slice
we are looking at is smooth, it is an ellipse.
This problem will appear more reasonable after we have looked at the role
of finite automata in the geometry
of Coxeter groups.)
|
|
A root
of a realization is the transform of one
of the basic roots by an element of W.
If b = w(as) is a root
then g s g-1 is reflection in the hyperplane
b = 0. Thus if b is a root so
is -b. The fundamental chamber C
of the representation is the intersection of all the root
half-spaces as > 0.
A root is called positive
if it contains the chamber C,
negative if its opposite contains C.
Proposition 16. Every root is either positive or negative.
The point is that the chamber C is not intersected by
a root hyperplane.
This result follows immediately from Theorem 3. A reformulation:
Proposition 17. If wC intersects C then w = 1.
Proof. If w is not equal to 1, then there exists s
with sw < w. But then C and wC lie on opposite
sides of the hyperplane as = 0.
In other words, every Cartan representation is a realization of the group
as a subgroup of GL(V). If we restrict the realization to
the subgroup generated by T, we see that
WT embeds into W, too.
For a subset T of S, let CT be the region in
the boundary of C where the basic roots at = 0 for
t in T, as > 0 for s not in T.
Every point of CT is fixed by t in T,
hence all elements of the subgroup WT. Conversely:
Proposition 18. 3. Let  be the closure of C.
If w be the closure of C.
If w intersects intersects  then the intersection equals the closure of
CT for some T, and w lies in WT. then the intersection equals the closure of
CT for some T, and w lies in WT.
Proof. By induction on l(w). If w = 0 or 1, no problem. Otherwise,
say sw < w and w = sx for l(x) < l(w). Then as  0 on x 0 on x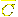 while aa
while aa 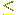 0 on w 0 on w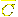 . Therefore the intersection
of C and wC lies in as = 0. But then
the intersection of x . Therefore the intersection
of C and wC lies in as = 0. But then
the intersection of x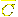 and and  is non-empty,
so we can apply the induction hypothesis. We deduce
that the intersection of x is non-empty,
so we can apply the induction hypothesis. We deduce
that the intersection of x and and  is equal to the
the closure of some CT, and x lies in WT.
But then sC intersects CT as well, and s lies in T also.
Hence w lies in WT. is equal to the
the closure of some CT, and x lies in WT.
But then sC intersects CT as well, and s lies in T also.
Hence w lies in WT.
Corollary. Any face of a chamber of a realization
is the W-transform of a unique face of C.
Proof. If xCU = yCT, then y-1xCU = CT.
But then y-1x must lie in WT.
In other words, each face of a chamber is labeled by
a unique subset T.
A gallery is a sequence of chambers Ci
with each successive pair sharing a face of codimension one. If
w = s1 ... sn then the sequence
C, s1C, s1s2C, ... , s1s2 ... snC is a gallery.
The chambers C and sC share a face labeled by s, and hence
wC and wsC do, too. Minimal galleries correspond to reduced words.
For w in W, let Lw be the set
of positive roots r such that w-1r is negative - i.e. r > 0
on C but r < 0 on wC. This means that the root hyperplane r = 0
separates C from wC. In any gallery
linking C to wC it must be one of the walls
between two successive chambers in the gallery. Therefore:
Proposition 19. The root hyperplanes for r in Lw
are those separating C from w-1C.
A minimal gallery from C through xC to xyC can be split into
two disjoint pieces, one from C to xC, the other from
xC to xyC. The second is the x-transform by x
of a gallery from C to yC. Therefore:
Proposition 20. If l(xy) = l(x) + l(y) then
Lxy is the disjoint union
of Lx and xLy.
Corollary. The length l(w) is the cardinality of Lw.
Corollary. The length of w is the number of root hyperplans
separating C from wC.
Proposition 21. An element w lies in WT if and only if
Lw is contained in T.
Let R+ be the set of positive roots,
RT those generated by WT from the at with t in T.
Proposition 22.
An element of WT permutes the roots in R+ - RT+.
Proposition 23. A reduced word for w in WT is one also in
W.
Proposition 24. In every coset WT \ W there exists a unique element
x such that tx > x for all t in T. For any w in this coset,
l(w) = l(wx-1) + l(x).
Let WT be the set of these distinguished coset representatives.
Proposition 25. Any element w can be expressed as w = xy
with x in WT and y in WT.
These last will be left as exercises.
|



 v) / (av
v) / (av  av)
av) 

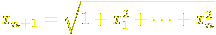
 / m
/ m




 /ms,t) .
/ms,t) .