- golden rectangles,
- Fibonacci numbers,
- regular pentagons,
- logarithmic spirals.
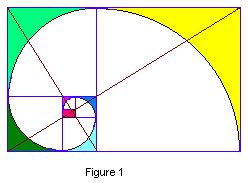
The picture on the right -- or some variation thereof -- occurs in many
books and web sites. The story behind it deals with such
totally diverse things as
|

|
Its main thrill lies in uncovering the invisible threads which connect these items. Its origins are lost in the mists of antiquity, with some parts as old as the Pyramids, others surfacing in Euclid's Elements (250 BC) and Ptolemy's Almagest (150 AD). The art-work by Leonardo da Vinci in Pacioli's Divina Proportione (1509 AD) helped spread its fame beyond the mathematical in-crowd.
Older accounts are entirely geometric, but with their fussy monochrome diagrams and awkward notation, they are difficult to follow. More recent versions, on the other hand, tend to achieve their brevity by an abundant use of algebraic formulas -- which most people find incomprehensible. The following pages will try to give a simple but complete account in the geometric vein and in full colour.
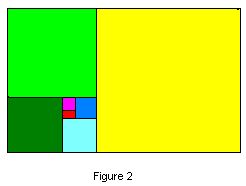
|
Figure 2 is a simplification of Figure 1. To recreate the latter,
you need only cut a quarter circle out of the yellow square,
another one out of the light green square, then the dark green square, and
so on -- and draw the brown diagonals in again.
Here you have a rectangle made up of smaller and smaller squares arranged in spiral fashion. This is known as a golden rectangle. |
A rectangle is golden if it has the following special property: when you cut a square (shown in yellow) away from it, you are left with a rectangle of the same shape -- so you can continue cutting off squares indefinitely.
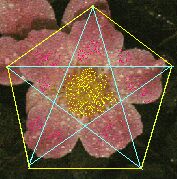
A rose is a rose is a rose -- and shares its pentagonal symmetry with
many other flowers, from buttercups to petunias. The underlying
pentagram (shown here in blue) is made up of golden triangles,
each of which is obtained from a golden rectangle by collapsing
one of the shorter sides.
This is the connection between golden rectangles and regular pentagons. |
 |
|
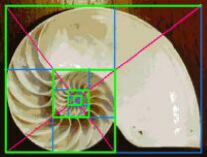
The nautilus, a tropical sea-shell, provides a beautiful example of a logarithmic spiral -- described by a point revolving around a center while at the same time moving outward exponentially (like the tip of a clock-hand which grows by compound interest). Hence it could just as well be called an exponential spiral. But people love the L-word -- it sounds so impressive -- and since it merely refers to the reverse way of looking at the same pattern, it is quite as legitimate as the E-word. |
The scaffolding for such a curve is given by a kind of rectangular spiral (shown here in green) wrapping around a rectangular cross (in red).
| Figure 3 reveals an analogous structure within the golden rectangle. In fact, if you start with any non-square rectangle, draw a diagonal and (from another corner) a perpendicular to it, and then wrap a rectangular spiral around the resulting cross, you always get the frame-work for some logarithmic spiral. Doing this with a golden rectangle, gives you a bonus: your spiral can now be approximated by a bunch of (easily drawn) quarter circles. | 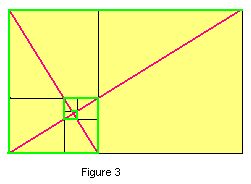
|
Alas, only approximated! The golden spiral shown in Figure 1 is not truly logarithmic -- it is not even smooth: if you were driving along it with constant speed, you would feel a sudden jerk in the steering wheel as you changed circles in passing from the yellow square to the green one.
So much for the geometric inhabitants of this zoo -- but what about Fibonacci and his numbers
|
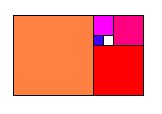
The truth is that the squares shown in Figure 2 are not in an ideal plane, but are actually made up of coloured dots (called "pixels"), and have sidelengths of 144, 89, 55, 34, 21 and 13 pixels, respectively -- rabbit numbers! The red rectangle stuck in the middle of Figure 2 measures 13-by-8 pixels, and when enlarged 10-fold looks like what you see on the left. |
If you continue to cut off squares, you will -- after 5 steps -- wind up with the white square. And then? In a truly golden rectangle you would be able to go on cutting squares indefinitely. So this is a fake -- but a close imitation! This is no coincidence, as we shall now see.