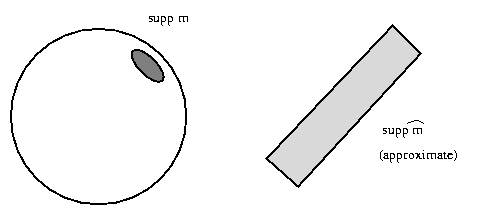The Kakeya problem, and connections to harmonic analysis



What is a Kakeya set?

Questions in harmonic analysis

The Kakeya conjecture

Further reading etc.

This page is meant to provide a very brief introduction to the Kakeya problem and some related questions. It was first posted in January 2001, and I expect that it will be evolving over time. For one thing, I will update it if further progress is made on the Kakeya conjecture. Also, I may include: descriptions of other problems, either related directly to Kakeya or just similar in spirit; more details about some of the ideas and methods involved; additional links, references, etc. If you have any comments or suggestions regarding this page, please write to ilaba@math.ubc.ca.

What is a Kakeya set?

A Besicovitch set is a subset of Rn which contains a unit line segment in each direction. Besicovitch sets are also known as Kakeya sets.

Besicovitch sets have an interesting history. In 1917 Besicovitch was working on a problem in Riemann integration, and reduced it to the question of existence of planar sets of measure 0 which contain a line segment in each direction. He then constructed such a set, and published his construction in a Russian journal in 1920.

Due to the civil war and the blockade, there was hardly any communication between Russia and the rest of the world at the time. (I was rather surprised to hear that anybody could be bothered to publish mathematical journals in Russia in 1920! But this is what Besicovitch says in Amer. Math. Monthly 70 (1963), 697-706.) Thus Besicovitch did not know that a Japanese mathematician Kakeya had asked, also in 1917, a somewhat related question: what is the smallest area of a convex set within which one can rotate a needle by 180 degrees in the plane? Pal (1921) resolved that problem (the convex set should be an equilateral triangle); the more interesting question, without the convexity assumption, remained open. Besicovitch was told of all this several years later, after he left Russia. By modifying his original construction, he gave the surprising answer that the area in question must of course be positive, but (with a lot of patience) may be made arbitrarily small. His solution was published in 1928.

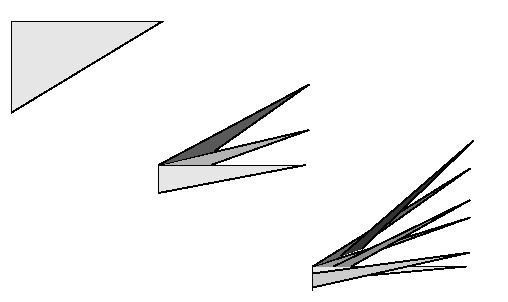
Many other ways to construct Besicovitch sets of measure zero have since been discovered (Perron, Schoenberg, Kahane,...). Most of them rely on the idea illustrated below. Essentially, we slice a triangle into many thin subtriangles, and then rearrange the latter so that they overlap a lot. If one does this carefully and then takes the limit as the number of subdivisions goes to infinity, one gets a Besicovitch set of measure 0 in the plane. Straightforward product techniques extend the construction to higher dimensions.



Questions in harmonic analysis

Kakeya sets (as well as a closely related construction due to Nikodym, 1927) have long been used to construct various counterexamples in analysis, starting with that Riemann integration problem considered by Besicovitch in 1917. Here I'm only going to describe two central problems in harmonic analysis - the restriction and Bochner-Riesz conjectures - which seem to depend on just how small Kakeya sets can really be. There are many other open problems in analysis, as well as PDE and number theory, involving Kakeya sets. (See the references in the "Further reading" section for more info.)

1. Convergence of Fourier series. In 1971, C. Fefferman used Besicovitch sets to construct a counterexample to the ball multiplier conjecture, which concerned a very basic problem in harmonic analysis. Let f be a function in Lp(Rn), and let F be its Fourier transform. If SR f ( x ) is the integral of F(k) exp(2 \pi i k x) over |k| < R, do SR f converge to f in Lp as R goes to infinity? It has long been known that Lp convergence holds for p = 2, and fails for p = 1 or infinity, in all dimensions. An old theorem of M. Riesz says that in dimension 1 the answer is yes for all finite p > 1, and a higher-dimensional analogue was generally expected to be true. However, Fefferman proved that in dimensions > 1 convergence fails for all p other than 2!

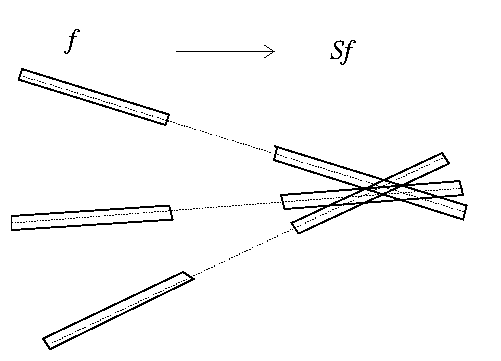
Fefferman's argument showcases a beautiful interplay between multidimensional Fourier analysis and Euclidean geometry. Here is how it goes. The problem is equivalent to checking whether the disc multiplier operator, which we will call S, is bounded on Lp(Rn). It now suffices to find functions f in Lp(Rn) such that the Lp norms of Sf are large. Fefferman does this by letting f be a sum of characteristic functions of long and thin tubes, multiplied by appropriate phase factors. It turns out that S essentially shifts each tube by a fixed distance in the "long" direction. Now suppose that the shifted tubes form something close to a Kakeya set; then the support of Sf is small, and so by Holder's inequality its Lp norm is large.



Now the disc multiplier question can be rewritten as follows. Let f and F be as above, and let g(k) be the characteristic funtion of the unit ball; does the inverse Fourier transform of F(k) g (k/R) converge to f in Lp(Rn) as R goes to infinity? Fefferman's result says that it is always so only for p=2. Yet if we let g to be e.g., a Gaussian instead, then the answer is yes for all finite p > 1 - this is the standard textbook proof of the Fourier inversion formula. So what happens if g(k) is somewhere in between? Where exactly does convergence start to fail?

The Bochner-Riesz conjecture, which looks essentially like a "regularized" version of the disc multiplier conjecture, deals with exactly this question. It is generally regarded as one of the major unsolved problems of harmonic analysis. (See Stein's book for a comprehensive discussion.) It turns out that Fefferman's construction would provide a counterexample to the Bochner-Riesz conjecture, if one could construct a Besicovitch set in Rn of Hausdorff dimension less than n. We will have much more to say about the latter question later on.

2. The restriction problem. Let f be a function in Lp(Rn), can we say anything intelligent about the restriction of the Fourier transform of f to a lower-dimensional subset E of Rn? If E is a hyperplane, then we can't - the Fourier transform of f does not even have to be defined on E. But if E is a curved surface, for example a sphere, then things are a bit different. There are deep results, due to Stein, Tomas, Fefferman, Bourgain, Wolff, and others, which say that for certain values of p and q the Fourier transform of f is actually in Lq(E). However, what has been proven is still quite far from what is being conjectured.

Again, the n-dimensional geometry plays a major role, and there is a point at which Kakeya sets become crucial (this time, via the uncertainty principle). Here is, very roughly, why. Let E=Sn-1 be the unit sphere. By duality, the restriction problem is equivalent to estimating the Lq' norm of the Fourier transform of measures supported on the sphere. Let m be such a measure concentrated on a very small spherical cap of diameter r. By uncertainty principle, its Fourier transform is essentially constant on a tube of length r-2 and diameter r-1, pointing in the direction perpendicular to the cap. Multiplying our measure m by a suitable phase factor, we can place this tube anywhere we like in the Fourier space.



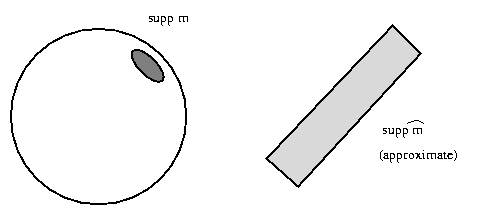
Now consider the sum of a large number of such measures, multiplied by phase factors chosen so that the corresponding Fourier tubes form an approximate Kakeya set. As in the disc multiplier argument, the Fourier transform of the whole thing has small support and therefore large Lp norms.

The restriction and Bochner-Riesz problems have long been known to be connected (e.g., partial results on both problems would often follow from the same oscillatory integral estimate). One can trace relevant research back to the 1930's, perhaps further. Many significant contributions are due to Stein, Calderon, Zygmund, Carleson, Sjolin, Fefferman, Hormander, Tomas, Cordoba, Christ, Sogge, Carbery, Bourgain, Wolff, Moyua, Tao, Vargas, Vega,... And it doesn't look like we'll be done with it any time soon.

The Kakeya conjecture

The problem below looks like geometric measure theory. The motivation for studying it comes from harmonic analysis, analytic number theory, and PDE. And the techniques used to prove the partial results stated below are mostly geometrical and combinatorial, additive number theory being the latest addition. It is generally expected that ideas from other, seemingly unrelated, fields of mathematics will be needed to finally resolve the problem. Anyone looking for opportunities for interdisciplinary research?

Conjecture. A Besicovitch set in Rn must have dimension n.

Naturally, one can ask what I mean by "dimension". There are several, not quite equivalent, definitions - those of interest to us are the Hausdorff and Minkowski dimension. Most mathematicians know what the Hausdorff dimension is. The Minkowski dimension (of a compact set) may be defined as follows. Let Eh be the h-neighbourhood of E in Rn, then the (upper) Minkowski dimension of E is the infimum of all a such that |Eh| < C hd-a for some constant C. The upper Minkowski dimension of a set is always greater or equal to its Hausdorff dimension, and there are examples of sets for which the inequality is strict.

There is also a stronger formulation of the conjecture in terms of maximal functions. The maximal function statements are actually quite important, as they are very closely related to the problems in analysis mentioned above. This is a bit more technical, though, so we will not go into it here - at least for now.

The conjecture is known to be true in dimension 2: the Hausdorff (hence also Minkowski) version was proved by Davies in 1971, and the maximal function version is due to Cordoba (1977) and Bourgain (1991). In higher dimensions it is still far from settled. Here is a brief summary of the best currently known lower bounds. Since there are no "less-or-equal" and "greater-or-equal" symbols in HTML, I will use <= and >=. Here are some of the ideas that went into proving the above results.

Further reading etc.

If you would like to learn more about Kakeya, here are some additional links and materials.

There are several recent expository articles on Kakeya and related topics:
Let's not forget about books.
I am also preparing Tom Wolff's Caltech lecture notes for publication. A revised version should be available here in a few weeks, and the whole book (including bibliographical notes etc.) should be finished by the end of the summer. Last semester I gave a series of lectures at UBC based on Wolff's notes - many thanks to everyone who attended!

Several people, including Ben Green and Terence Tao, have posted expository Kakeya articles and lecture notes on their web pages. These are worth checking out, though I don't necessarily agree with everything they say.

If you need more details, you will have to look up the original research articles. Many of them are available online from the Los Alamos preprint archive at http://xxx.lanl.gov. They can also be downloaded from the UC Davis server at http://front.math.ucdavis.edu. Some time I might look up the links and put them here.

And did I say that there is plenty of ongoing research on these and related subjects? I will try to keep this page up-to-date and add new links and references as they appear. :-)


Last updated August 26, 2002.