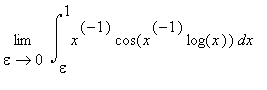 ?
?
What is
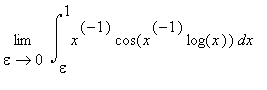 ?
?
Solution:
Use a change of variables
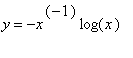 to make the cosine linear in the variable of integration.
to make the cosine linear in the variable of integration.
| > | restart; |
| > | ti:= time(): Digits:= 20: |
| > | J:= Int(x^(-1)*cos(x^(-1)*ln(x)),x=epsilon..1); |
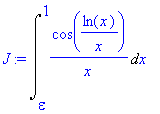
| > | alias(W=LambertW): xs:= solve(y=-x^(-1)*ln(x),x); |
![]()
| > | simplify(PDEtools[dchange](x=xs,J)); |
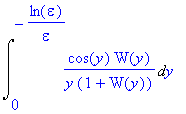
Of course,
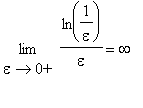 .
.
| > | integrand:= cos(y)*LambertW(y)/(1+LambertW(y))/y; |
![]()
| > | answer:= Int(integrand,y=0..infinity); |
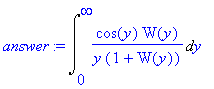
This is still not a very pleasant oscillatory integral, although the singularity at 0 is removable. We break it up into 3 pieces. For y from 0 to
![]() , use ordinary numerical integration, (but on the original form of the integral, to avoid the apparent singularity at y=0 as well as not having to evaluate W numerically; and using the _Dexp method, as otherwise Maple will have trouble because it's close to the singularity at
, use ordinary numerical integration, (but on the original form of the integral, to avoid the apparent singularity at y=0 as well as not having to evaluate W numerically; and using the _Dexp method, as otherwise Maple will have trouble because it's close to the singularity at
![]() ).
).
| > | Int(1/x * cos(ln(x)/x) , x=subs( y=199*Pi, xs ) ... 1 ); r1:= evalf(Int(op(%),_Dexp)); |
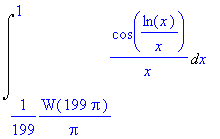
![]()
For each interval
![]()
![]() for
for
![]() , write the integral as
, write the integral as
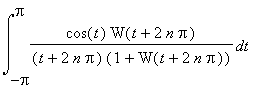 . Expand this in an asymptotic series in n and integrate term-by-term. The terms for even n vanish by symmetry.
. Expand this in an asymptotic series in n and integrate term-by-term. The terms for even n vanish by symmetry.
| > | map(factor,asympt(cos(t)*W(t+2*n*Pi)/(t+2*n*Pi)/(1+W(t+2*n*Pi)), n, 8)); |
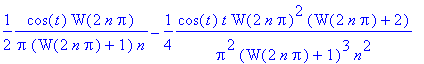
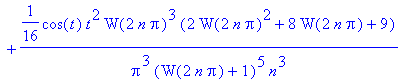
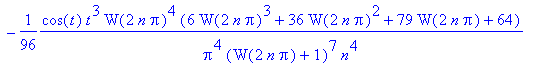
![]()
![]()
![]()
![]()
![]()
![]()
![]()
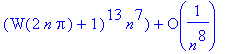
| > | J2:= map(factor,map(int, eval(%,O=0), t=-Pi..Pi)); |
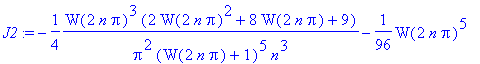
![]()
![]()
![]()
![]()
![]()
| > | L:= convert(%,list): evalf(eval(L,n=100)); |
![]()
![]()
Apparently by
![]() we only need the
we only need the
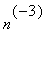 and
and
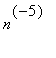 terms. We'll use these for n from 100 to 1000.
terms. We'll use these for n from 100 to 1000.
| > | J3:= op(1,J2)+op(2,J2); r2:= add(evalf(J3),n=100..1000); |
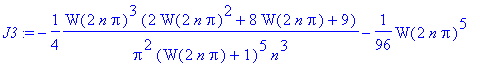
![]()
![]()
![]()
For n > 1000, use the asymptotics of the Euler-Maclaurin form for the summation of the
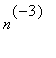 and
and
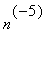 terms.
terms.
| > | J4:= map(factor,asympt(eulermac(J3,n),n)); |
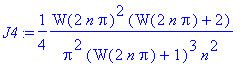
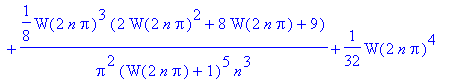
![]()
![]()
![]()
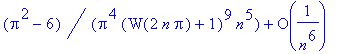
| > | r3:= -evalf(eval(J4,{O=0, n=1001})); |
![]()
| > | r:= r1+r2+r3; |
![]()
Actual answer, as given by Trefethen to 40 digits:
0.3233674316 7777876139 9370087952 1704466510...
| > | (time()-ti)*seconds; |
![]()