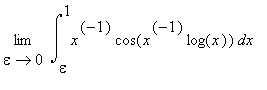 ?
?
Solutions to the SIAM 100-Dollar, 100-Digit Challenge
This file was exported from a Maple worksheet.
Team: Gaston Gonnet, Informatik, ETH, Zurich, and Robert Israel, Mathematics, UBC.
Most of these solutions are the ones that actually produced the results we
sent in, but I (R.I.) have changed a few of them. All these
solutions use Maple.
Each problem had an answer that was a single real number, of which 10 correct digits were required.
The complete results are at http://www.comlab.ox.ac.uk/oucl/work/nick.trefethen/hundred.html. Our team was one of 20 first prize winners. See our prize.
Problem 1:
What is
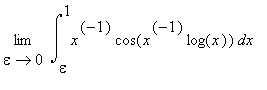 ?
?
Problem 2:
A photon moving at speed 1 in the
![]() plane starts at
plane starts at
![]() at
at
![]() heading due east. Around every integer lattice point
heading due east. Around every integer lattice point
![]() in the plane, a circular mirror of radius
in the plane, a circular mirror of radius
![]() has been erected. How far from the origin is the photon at
has been erected. How far from the origin is the photon at
![]() ?
?
Problem 3:
The infinite matrix
![]() with entries
with entries
![]() ,
,
![a[1,2] = 1/2](images/challenge157.gif) ,
,
![a[2,1] = 1/3](images/challenge158.gif) ,
,
![a[1,3] = 1/4](images/challenge159.gif) ,
,
![a[2,2] = 1/5](images/challenge160.gif) ,
,
![a[3,1] = 1/6](images/challenge161.gif) , etc., is a bounded operator on
, etc., is a bounded operator on
![]() . What is ||
. What is ||
![]() ||?.
||?.
Problem 4:
What is the global minimum of the function
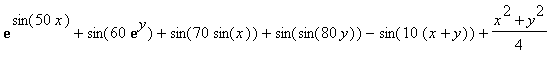 ?
?
Problem 5:
Let
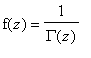 , where
, where
![]() is the gamma function, and let
is the gamma function, and let
![]() be the cubic polynomial that best approximates
be the cubic polynomial that best approximates
![]() on the unit disk in the supremum norm
on the unit disk in the supremum norm
![]() . What is
. What is
![]() ?
?
Problem 6:
A flea starts at (0,0) on the infinite 2D integer lattice and executes a biased random walk: At each step it hops north or south with probability 1/4, east with probability
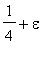 , and west with probability
, and west with probability
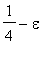 . The probability that the flea returns to (0,0) sometime during its wanderings is 1/2. What is
. The probability that the flea returns to (0,0) sometime during its wanderings is 1/2. What is
![]() ?
?
Problem 7:
Let
![]() be the 20,000 x 20,000 matrix whose entries are zero everywhere except for the primes 2, 3, 5, 7, ..., 224737 along the main diagonal and the number 1 in all the positions
be the 20,000 x 20,000 matrix whose entries are zero everywhere except for the primes 2, 3, 5, 7, ..., 224737 along the main diagonal and the number 1 in all the positions
![]() with
with
![]() ,2,4,8,...,16384. What is the (1,1) entry of
,2,4,8,...,16384. What is the (1,1) entry of
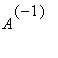 ?
?
Problem 8:
A square plate
![]() x
x
![]() is at temperature
is at temperature
![]() . At time
. At time
![]() the temperature is increased to
the temperature is increased to
![]() along one of the four sides while being held at
along one of the four sides while being held at
![]() along the other three sides, and heat then flows into the plate according to
along the other three sides, and heat then flows into the plate according to
![]() . When does the temperature reach
. When does the temperature reach
![]() at the center of the plate?
at the center of the plate?
Problem 9:
The integral
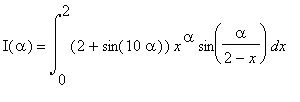 depends on the parameter
depends on the parameter
![]() . What is the value
. What is the value
![]() at which
at which
![]() achieves its maximum?
achieves its maximum?
Problem 10:
A particle at the center of a 10 x 1 rectangle undergoes Brownian motion (i.e. 2D random walk with infinitesimal step lengths) till it hits the boundary. What is the probability that it hits at one of the ends rather than at one of the sides?