![a[1,2] = 1/2](images/challenge157.gif) ,
,
![a[2,1] = 1/3](images/challenge158.gif) ,
,
![a[1,3] = 1/4](images/challenge159.gif) ,
,
![a[2,2] = 1/5](images/challenge160.gif) ,
,
![a[3,1] = 1/6](images/challenge161.gif) , etc., is a bounded operator on
, etc., is a bounded operator on
The infinite matrix
![]() with entries
with entries
![]() ,
,
![a[1,2] = 1/2](images/challenge157.gif) ,
,
![a[2,1] = 1/3](images/challenge158.gif) ,
,
![a[1,3] = 1/4](images/challenge159.gif) ,
,
![a[2,2] = 1/5](images/challenge160.gif) ,
,
![a[3,1] = 1/6](images/challenge161.gif) , etc., is a bounded operator on
, etc., is a bounded operator on
![]() . What is ||
. What is ||
![]() ||?.
||?.
Solution:
The norm is the square root of the largest eigenvalue of
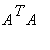 , which can be computed by a simple iteration:
, which can be computed by a simple iteration:
Start with a "typical" vector
![]() , normalized so
, normalized so
![]() , and repeat
, and repeat
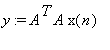
![x(n+1) := y/y[1]](images/challenge168.gif)
Then
![]() converges to the largest eigenvalue (the second eigenvalue is much smaller, so it converges quite fast). But we can only work with a finite number of components, so we truncate to an m by m matrix. I did it in Maple for up to a 2500 by 2500 matrix (obtaining 1.274224152 5171129126 which happens to have 10 correct digits, but I wasn't confident of the 10th), and Gaston used a C program to get the result for a 32768 by 32768 matrix (of course we don't actually construct the matrix, but work directly with vectors). His result was 1.274224152 82109, which has 13 correct digits.
converges to the largest eigenvalue (the second eigenvalue is much smaller, so it converges quite fast). But we can only work with a finite number of components, so we truncate to an m by m matrix. I did it in Maple for up to a 2500 by 2500 matrix (obtaining 1.274224152 5171129126 which happens to have 10 correct digits, but I wasn't confident of the 10th), and Gaston used a C program to get the result for a 32768 by 32768 matrix (of course we don't actually construct the matrix, but work directly with vectors). His result was 1.274224152 82109, which has 13 correct digits.
Here's the Maple code.
| > | mulAA:= proc(V::Array,W::Array,n) # multiply the n-component vector V by A^T*A # W is another vector of the same size used for # intermediate calculations local i,j; for i from 1 to n do W[i]:= add(V[j]/((i+j-1)*(i+j-2)/2+i),j=1..n) od; for j from 1 to n do V[j]:= add(W[i]/((i+j-1)*(i+j-2)/2+i),i=1..n) od; end: |
| > | F:= proc(n) # get the approximate eigenvalue for an n x n # truncation local V,W,VP,i,eps; if not type(n,integer) then return 'procname(n)' fi; eps:= 1.0*10^(-Digits+4); V:= Array(1..n,datatype=float[8]); W:= Array(1..n,datatype=float[8]); V[1]:= 1.0; for i from 2 to n do V[i]:= 0 od; do VP:= copy(V); mulAA(V,W,n); if max(seq(abs(V[i]-V[1]*VP[i]),i=1..n)) < eps then return sqrt(V[1]) fi; for i from 2 to n do V[i]:= V[i]/V[1] od; V[1]:= 1.0; od; end: |
| > | Digits:= 15: ti:= time(): F(20); (time()-ti)*seconds; ti:= time(): F(200); (time()-ti)*seconds; |
![]()
![]()
![]()
![]()
Some groups used various extrapolation techniques. We didn't.
Back to Solutions to the SIAM $100 Challenge