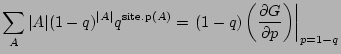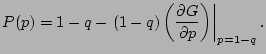Next: Partitions of integers and
Up: Why do we want
Previous: Why do we want
Percolation models
Percolation theory was introduced by Broadbent and Hammersley [7] as a
mathematical model (or a collection of mathematical models) of random media. Consider the
square grid; let each site be ``occupied'' with probability 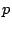 or ``vacant'' with
probability
or ``vacant'' with
probability 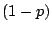 , independently of all the other sites on the lattice. A ``percolation
cluster'' on this grid is a collection of nearest-neighbour occupied sites -- a site
animal! The number of occupied sites within a cluster is called its ``mass'' (see
figure 15). Instead of occupying the sites on the lattice, we can also
consider occupying the bonds or a combination of both -- giving rise to site-percolation,
bond-percolation and site-bond-percolation. Percolation clusters can (and have) been used
to model a wide array of phenomena; from oil deposits to forest fires (see
[38,17] and references therein)
, independently of all the other sites on the lattice. A ``percolation
cluster'' on this grid is a collection of nearest-neighbour occupied sites -- a site
animal! The number of occupied sites within a cluster is called its ``mass'' (see
figure 15). Instead of occupying the sites on the lattice, we can also
consider occupying the bonds or a combination of both -- giving rise to site-percolation,
bond-percolation and site-bond-percolation. Percolation clusters can (and have) been used
to model a wide array of phenomena; from oil deposits to forest fires (see
[38,17] and references therein)
Figure 15:
Percolation clusters: five clusters of mass 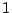 , one of mass
, one of mass 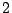 , two of mass
, two of mass
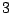 and two of mass
and two of mass 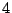 .
.
|
|
As the occupation probability, 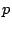 , is increased from zero, the average or typical
clusters become larger (both in terms of the number of sites and geometric size). If we
define
, is increased from zero, the average or typical
clusters become larger (both in terms of the number of sites and geometric size). If we
define 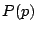 , ``the percolation probability'', to be the probability that the origin is
part of an infinite cluster, then we find that below a certain value
, ``the percolation probability'', to be the probability that the origin is
part of an infinite cluster, then we find that below a certain value 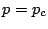 ,
called the critical probability,
,
called the critical probability, 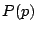 is always zero. As
is always zero. As 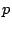 is increased above
is increased above 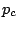 ,
the percolation probability becomes non-zero (see figure 16). This change in
behaviour is an example of a phase transition.
,
the percolation probability becomes non-zero (see figure 16). This change in
behaviour is an example of a phase transition.
Figure 16:
The expected behaviour of the percolation probability, 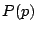 .
.
|
|
As an example consider an orchard, in which all of the trees are arranged on the vertices
of a large square grid. Suppose that a tree will become infected with a nasty disease with
probability 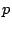 if one of its neighbours is infected. Say a few of the trees in the orchard
become infected and the disease spreads through the orchard. After a few days the disease
has stopped spreading and there are a number of clusters of diseased trees. Obviously, in
this scenario we wish to minimise the size of these clusters; if we know how
if one of its neighbours is infected. Say a few of the trees in the orchard
become infected and the disease spreads through the orchard. After a few days the disease
has stopped spreading and there are a number of clusters of diseased trees. Obviously, in
this scenario we wish to minimise the size of these clusters; if we know how 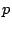 varies
with the distance between trees (presumably it decreases as we place trees further apart),
how far apart do we have to plant the trees to stop the epidemic from destroying a large
portion of the orchard? We could just place the trees a long way apart (a small value of
varies
with the distance between trees (presumably it decreases as we place trees further apart),
how far apart do we have to plant the trees to stop the epidemic from destroying a large
portion of the orchard? We could just place the trees a long way apart (a small value of
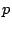 ), but then there would not be many trees in the orchard and we would go broke. For the
orchard to be viable we need lots of trees, and so we need to choose a large value of
), but then there would not be many trees in the orchard and we would go broke. For the
orchard to be viable we need lots of trees, and so we need to choose a large value of 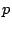 ,
but not so large that the orchard is endangered. If
,
but not so large that the orchard is endangered. If 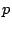 is chosen below the critical
probability, then we know that the average cluster size will be quite small, and the
disease cannot spread far. On the other hand, if
is chosen below the critical
probability, then we know that the average cluster size will be quite small, and the
disease cannot spread far. On the other hand, if 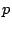 is above the critical
probability, then there is a non-zero probability that the disease could spread to a
significant part of the orchard. Hence we must choose
is above the critical
probability, then there is a non-zero probability that the disease could spread to a
significant part of the orchard. Hence we must choose 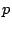 as close to
as close to 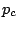 as we dare,
while still ensuring that
as we dare,
while still ensuring that 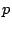 is less than
is less than 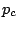 .
.
The percolation probability, 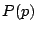 , can be written in terms of site animals enumerated
according to their area and another parameter, the site-perimeter. The
site-perimeter of a site animal is the number of nearest-neighbour sites that are not part
of the animal (see figure 17).
, can be written in terms of site animals enumerated
according to their area and another parameter, the site-perimeter. The
site-perimeter of a site animal is the number of nearest-neighbour sites that are not part
of the animal (see figure 17).
Figure 17:
A site animal and its site-perimeter. This animal contains 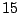 sites, and
has a site-perimeter of
sites, and
has a site-perimeter of 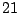 .
.
|
|
Let us write the generating function of all finite site animals, 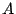 , enumerated
according to both area and site-perimeter as
, enumerated
according to both area and site-perimeter as
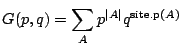 |
(6) |
where 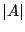 and
site.p
and
site.p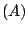 denote, respectively, the area and site-perimeter of an
animal
denote, respectively, the area and site-perimeter of an
animal 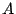 . The probability that the origin is part of a given cluster
. The probability that the origin is part of a given cluster 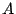 is equal to
is equal to
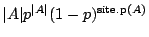 , since
, since 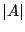 sites must be occupied,
site.p
sites must be occupied,
site.p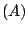 sites must be vacant, and there are exactly
sites must be vacant, and there are exactly 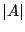 ways of
placing the animal over the origin. Consequently the probability that the origin is part
of a finite cluster is (expanding in
ways of
placing the animal over the origin. Consequently the probability that the origin is part
of a finite cluster is (expanding in 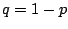 about
about 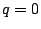 )
)
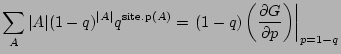 |
(7) |
and the percolation probability is the probability that the origin is not part of a
finite cluster (nor vacant):
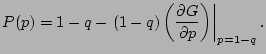 |
(8) |
So a knowledge of 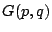 would give us an expression for
would give us an expression for 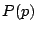 . Unfortunately
computing the site-perimeter of polyominoes is a very difficult problem; to date,
only polygons that are fully convex (rectangles, Ferrers diagrams, stacks, staircase
polygons, directed convex polygons and convex polygons) have been solved by
site-perimeter. In chapter 6 we find the site-perimeter generating
function of the simplest family of non-convex polygons -- bargraph polygons.
. Unfortunately
computing the site-perimeter of polyominoes is a very difficult problem; to date,
only polygons that are fully convex (rectangles, Ferrers diagrams, stacks, staircase
polygons, directed convex polygons and convex polygons) have been solved by
site-perimeter. In chapter 6 we find the site-perimeter generating
function of the simplest family of non-convex polygons -- bargraph polygons.



Next: Partitions of integers and
Up: Why do we want
Previous: Why do we want
Andrew Rechnitzer
2002-12-16
![% latex2html id marker 3738
\includegraphics[scale=0.6]{figs/perc1.eps}](img106.png)
![% latex2html id marker 3738
\includegraphics[scale=0.6]{figs/perc1.eps}](img106.png)
![]() , is increased from zero, the average or typical
clusters become larger (both in terms of the number of sites and geometric size). If we
define
, is increased from zero, the average or typical
clusters become larger (both in terms of the number of sites and geometric size). If we
define ![]() , ``the percolation probability'', to be the probability that the origin is
part of an infinite cluster, then we find that below a certain value
, ``the percolation probability'', to be the probability that the origin is
part of an infinite cluster, then we find that below a certain value ![]() ,
called the critical probability,
,
called the critical probability, ![]() is always zero. As
is always zero. As ![]() is increased above
is increased above ![]() ,
the percolation probability becomes non-zero (see figure 16). This change in
behaviour is an example of a phase transition.
,
the percolation probability becomes non-zero (see figure 16). This change in
behaviour is an example of a phase transition.
![]() if one of its neighbours is infected. Say a few of the trees in the orchard
become infected and the disease spreads through the orchard. After a few days the disease
has stopped spreading and there are a number of clusters of diseased trees. Obviously, in
this scenario we wish to minimise the size of these clusters; if we know how
if one of its neighbours is infected. Say a few of the trees in the orchard
become infected and the disease spreads through the orchard. After a few days the disease
has stopped spreading and there are a number of clusters of diseased trees. Obviously, in
this scenario we wish to minimise the size of these clusters; if we know how ![]() varies
with the distance between trees (presumably it decreases as we place trees further apart),
how far apart do we have to plant the trees to stop the epidemic from destroying a large
portion of the orchard? We could just place the trees a long way apart (a small value of
varies
with the distance between trees (presumably it decreases as we place trees further apart),
how far apart do we have to plant the trees to stop the epidemic from destroying a large
portion of the orchard? We could just place the trees a long way apart (a small value of
![]() ), but then there would not be many trees in the orchard and we would go broke. For the
orchard to be viable we need lots of trees, and so we need to choose a large value of
), but then there would not be many trees in the orchard and we would go broke. For the
orchard to be viable we need lots of trees, and so we need to choose a large value of ![]() ,
but not so large that the orchard is endangered. If
,
but not so large that the orchard is endangered. If ![]() is chosen below the critical
probability, then we know that the average cluster size will be quite small, and the
disease cannot spread far. On the other hand, if
is chosen below the critical
probability, then we know that the average cluster size will be quite small, and the
disease cannot spread far. On the other hand, if ![]() is above the critical
probability, then there is a non-zero probability that the disease could spread to a
significant part of the orchard. Hence we must choose
is above the critical
probability, then there is a non-zero probability that the disease could spread to a
significant part of the orchard. Hence we must choose ![]() as close to
as close to ![]() as we dare,
while still ensuring that
as we dare,
while still ensuring that ![]() is less than
is less than ![]() .
.
![]() , can be written in terms of site animals enumerated
according to their area and another parameter, the site-perimeter. The
site-perimeter of a site animal is the number of nearest-neighbour sites that are not part
of the animal (see figure 17).
, can be written in terms of site animals enumerated
according to their area and another parameter, the site-perimeter. The
site-perimeter of a site animal is the number of nearest-neighbour sites that are not part
of the animal (see figure 17).
![% latex2html id marker 3792
\includegraphics[scale=0.6]{figs/perc3.eps}](img110.png)