


Next: Polymer models
Up: Why do we want
Previous: Percolation models
One of the simplest and most natural mathematical operations is the adding of
integers. Integer partitions describe the ways in which a positive integer can be written as
the sum of other positive integers. For example the number 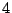 can be written as
So there are
can be written as
So there are 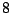 ways of writing the number
ways of writing the number 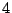 as a sum of positive integers. These
as a sum of positive integers. These 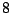 different sums are compositions.
different sums are compositions.
Definition 9
A composition of a positive integer 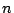 is an ordered finite sequence of positive
integers
is an ordered finite sequence of positive
integers
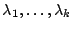 such that
such that
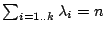 .
.
Implicit in this definition is that we care about the order in which the
summands appear; the composition 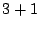 is not the same as
is not the same as 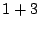 . Since addition is
commutative, this distinction seems a little artificial, and it would be more natural to
consider the compositions
. Since addition is
commutative, this distinction seems a little artificial, and it would be more natural to
consider the compositions 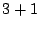 and
and 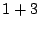 to be the same object. One way of ensuring this
is to require the summands to be in non-increasing order -- this leads us to partitions.
to be the same object. One way of ensuring this
is to require the summands to be in non-increasing order -- this leads us to partitions.
Definition 10
A partition of a positive integer 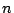 is a finite sequence of
non-increasing positive integers
is a finite sequence of
non-increasing positive integers
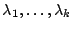 such that
such that
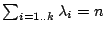 .
.
Using this we find that there are 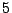 partitions of the number
partitions of the number 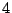 .
.
There is a vast array of combinatorial and algebraic structure to be explored in the
theory of partitions, far more than we have time for here (see [1] for more
on this subject). Instead let us consider the graphical representation of partitions and
compositions.
Let us represent a positive integer, 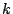 , by a column of
, by a column of 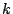 cells. A sequence of
positive integers is represented by a sequence of columns. In this way every composition can be
uniquely represented by a sequence of columns of cells -- the total number of cells is
the total of the composition (see figure 18).
cells. A sequence of
positive integers is represented by a sequence of columns. In this way every composition can be
uniquely represented by a sequence of columns of cells -- the total number of cells is
the total of the composition (see figure 18).
Figure 18:
Representing the 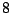 compositions of the number
compositions of the number 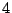 by sequences of columns.
by sequences of columns.
|
|
These sequences of columns are bargraph polygons and so the number of compositions of 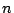 is equal to the number of bargraph polygons of area
is equal to the number of bargraph polygons of area 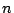 .
.
Figure 19:
Representing the 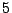 partitions of the number
partitions of the number 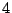 by sequences of columns.
by sequences of columns.
|
|
If we consider partitions instead of compositions, then the sequence of columns must be
non-increasing -- this gives us Ferrers diagrams (see figure 19).
Generalising this idea, we consider other subsets with other conditions; for example, if
we require that the sequence be unimodal then we obtain stack polygons. Polyominoes can
be seen as a generalisation of these objects.



Next: Polymer models
Up: Why do we want
Previous: Percolation models
Andrew Rechnitzer
2002-12-16
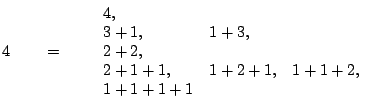
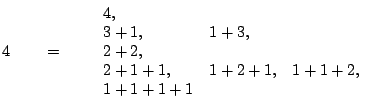
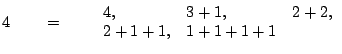
![]() , by a column of
, by a column of ![]() cells. A sequence of
positive integers is represented by a sequence of columns. In this way every composition can be
uniquely represented by a sequence of columns of cells -- the total number of cells is
the total of the composition (see figure 18).
cells. A sequence of
positive integers is represented by a sequence of columns. In this way every composition can be
uniquely represented by a sequence of columns of cells -- the total number of cells is
the total of the composition (see figure 18).