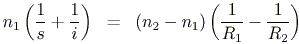
We reiterate some of the important points made in this section of our work. Our results are valid for spherical mirrors and lenses, for sources close to the optical axis.

Let Side A of an optical component be the side from which light starts, and let Side B be the side to which light travels. With mirrors, Sides A and B are identical. If s is the source distance, i is the image distance, R is the radius of curvature, and f is the focal length, then, our sign conventions are as follows.

• The sign of s is determined by Side A. If the source is on Side A, s is positive; if it is on the side opposite to Side A, s is negative.
• The signs of i, R, f are determined by Side B. For the image and the focal point, their measurements are positive if they are on Side B, and negative if they are on the side opposite to Side B. R is positive provided the centre of curvature is on Side B; it will be negative if it is on the side opposite Side B.

For mirrors, the source distance s, image distance i, and focal length f satisfy the equation

For lenses, they satisfy the equation

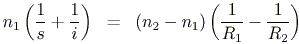
where n₁ is the index of refraction for the region surrounding the lens, and n₂ is the index for the lens itself. R₁ and R₂ are the radii of curvature for the first and second surfaces of the lens respectively. In air, this equation reduces to the lens-makers' equation,

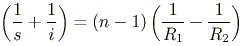
where n is the index of the lens.

The focal length of a mirror is very nearly half of its radius,

For a thin lens, the focal length is found using the image-source equation, taking s to approach infinity. In air, the symmetric foci of a lens are f units away from the lens, where f satisfies

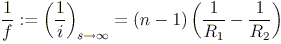
The magnification of a mirror or a lens is the ratio of the image distance to the source distance,

M is negative if the image is upside down, and positive if it is right side up.