|
|
Magnifying Power (brief overview)
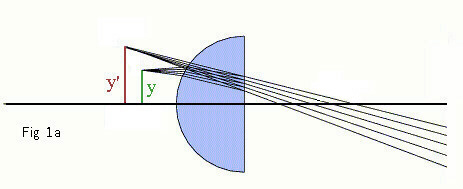
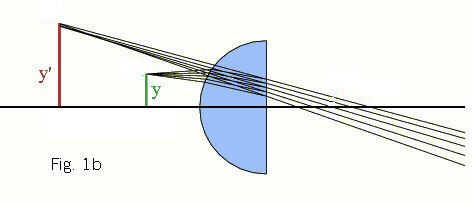
Magnifying power: is also called angular magnification. Figure 1a
shows an object y in front of a lens. Rays of light reflect off the object
through the lens and a now larger image, y', of y can be seen. Once, the
image is brought further from the lens, as in figure 1b, the image, y', is
even larger. (So as to no discrepency: in figures 1a and 1b, the observer is
on the right of the lens looking towards the image y')
The magnifying power, M, is given by the following:
M = 1 + d/f, where f is the focal distance and d is the distance between the
object and the lens |
|
Proof of M = 1 + d/f:
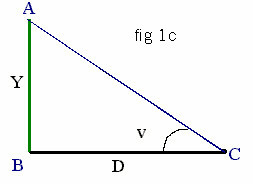 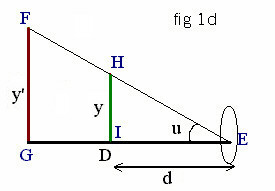
Figure 1c is the view of the object Y from point C without a magnifying
glass.
Figure 1d is the view of the object y from point E with a magnifying
glass.
let:
- M = magnification
- y, Y = object
- D = distance between object and lens (within focal length - if
beyond focal length you get a virtual image)
- y' = image
- d = distance between image and lens
- f = focal length
by definition, M = u/v
Since u and v are small, let u = tanu and v = tanv
Thus M = tanu / tanv (1)
In the figure 1c, triangle ABC is right; thus tanv = Y/D (2)
Right triangle HIE gives tanu = y/d
Since y = Y, tanu = Y/d (3)
Thus, substituting (2) and (3) into (1) you get M = (Y/d) / (Y/D) = D/d
Substituting into the thin lens formula: 1/f = -1/D + 1/d
Multiplying both sides by D: D/f = -1 + D/d, and adding one to both
sides: D/d = 1 + D/f = M |
Total magnification can be found by: M1 x M2 = M(total), where M1 and M2 are
magnifications
Thus, in a compound microscope (a microscope with more than one lens) the
magnification can be found by:
M(total)= M1 x M2 where M1 = -L/f(o) = magnification of the objective, M2 =
1 + D/f(e) = magnification of eyepiece (f(o)= focal point of objective, f(e)
= focal point of eye piece, L = distance between the two lenses, D =
distance between object and first lens)
Thus M = (-L/f(o)) + (1 + D/f(e))*
*The negative sign means the image seen is upside down.
Notes:
|
|