Resolving Power (Page 1) Numerical aperture, NA, is the "half-angle subtended at the object by the entrance pupil of the system (usually the first lens) and the index of the viewing medium" (Blaker, Geometric Optics the Matrix Theory). Allowing n = refractive index of the object, and u = angle of the cone of light coming from the objective, the numerical aperture can be found by NA = n sinu. What is the largest NA? NA = nsinu; thus, we want the largest n and largest sinu. As will be explained later, the maximum sinu is 0.95. The index of refraction in air is 1.0 and the index of refraction of oil and glass cover (ie lens dipped in oil) is 1.515. Thus, using n = 1.515, the "largest" NA can be found: NA = (1.515)(0.95) = 1.44 The limiting angle of resolution, u(min), with an objective diameter of b is given by the equation: u(min) = 1.22λ / b "Proof" of u(min) = 1.22λ / b: let:   a = width of the slit u = angle of deflection u(min) = angle of limiting resolution b = diameter of lens λ = wavelength As seen in figure 7*, ray1 travels a/2 sinu further than ray 3 (ray 2 and ray 3 travel a/2 sinu further than ray 4 and ray 5 respectively) 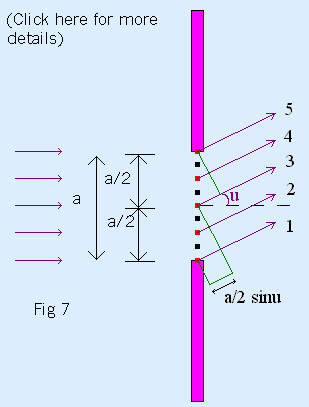There is destructive interference (the viewing screen is dark) when: a/2 sinu = λ / 2 Therefore, sin u = λ / a However, λ is very small (around 5*10^(-9)) so u is approximately equal to sinu. Thus, it can be written: u(min) = λ / a However, microscopes are not slits (they are circulare apertures) so u(min) must be greater if the image is to be resolved. Many experiments have been performed to find out just how much larger this u(min) must be, their results showed that it must be 1.22 times larger. Thus, replacing the width of the slit with the diameter of the lens and increasing u(min) by a factor of 1.22, we get: u(min) = 1.22 λ / b *this figure is modelled after Figure 38.5 in Physics for Scientists and Engineers by Serway The limiting angle of resolution can be decreased when: the diameter of the lens, b, is increased decreasing the wavelength, λ (ie by using filteres) Note: Theoretically, the largest value of u should be 90 degrees (assuming the lens was large enough); however, in practice, the maximum view is only about 71.8 degrees (ie sinu = 0.95). Even though 71.8 degrees is the maximum angle that can be obtained, it is every difficult to achieve such a high u since equipment and environment must be ideal. How can you minimize the limiting angle of resolution of a lens which has a diameter of 0.900cm? By using the smallest visible light wave, which is 400nm, and immersing the object in oil (which has a refraction index, n, of about 1.5) the smallest limiting angle of resolution, u(min), can be found: λ(oil) = λ(air) / λ(oil) = 400nm / 1.5 = 268nm u(min) = 1.22 λ / b = 1.22(0.0000267cm / 0.900cm) = 0.0000362 radians