Dr. Neil Balmforth
RESEARCH INTERESTS
Large Dynamical Systems:
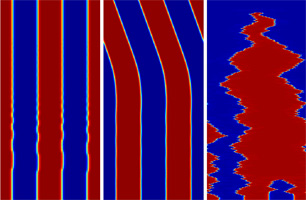
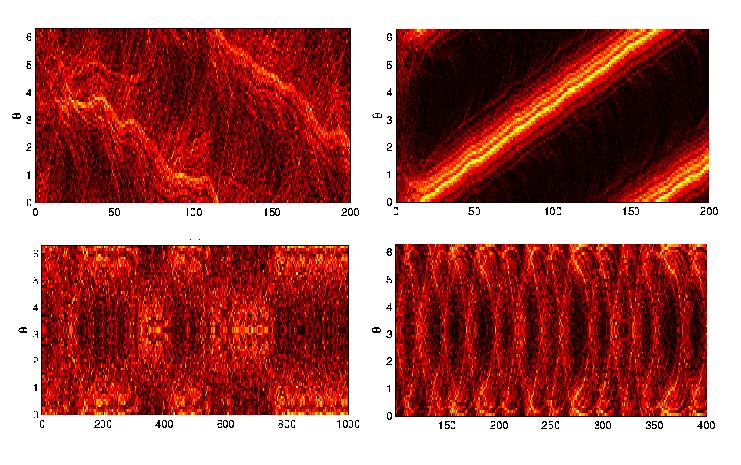
The atmosphere or the ocean is an extremely large dynamical system with many degrees of freedom. This size makes it impractical to model these systems on a first principles basis without some severe approximations. Morever, state-of-the-art models are highly complicated dynamical systems themselves, which makes it challenging to assess the robustness of the models to variations in all the input parameters and physics, and to test methods of reconstruction and prediction. Instead, one can work with smaller, more accessible systems to examine the viability of a physical process or the utility of a technical method. One option is to gradually build up large complex systems by coupling together a number of much simpler subsystems. These coupled ensembles act as metaphors for the complex systems that we encounter in nature. For example, ensembles of coupled oscillators can be use to explore the phenomenon of synchronization that is observed in biological populations such as flashing fireflies and cooperative cells. And with lattices of coupled maps and simple chaotic systems, one can test the feasibility of unravelling and reconstructing the underlying governing dynamics from an observed signal.
My collaborators in these efforts include Antonello Provenzale, Roberto Sassi and Ed Spiegel
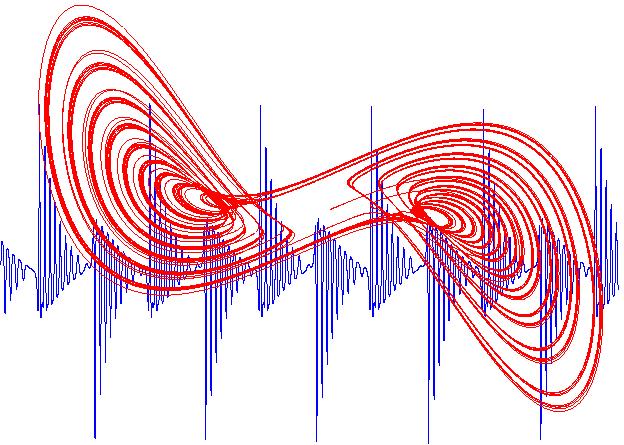
(phase portrait and time series of the Moore-Spiegel strange attractor)