Most multi-scale embedding schemes (A/C, QM/MM, . . .) schemes can be understood within a single framework: a coarse model for a far-field is used to provide a boundary condition for a core region of interest. It turns out that, for crystalline defects, boundary conditions of arbitrary accuracy can be constructed almost analytically, without ever having to resort to the complex mechanisms and many pitfalls of concurrent multi-scale schemes. We achieve this by constructing an expansion of an atomistic model in terms of higher-order continuum models and then extracting an effective far-field model at the desired accuracy. We then prescribe a self-consistent equation coupling the defect core to the far-field.

The starting point is a multi-pole expansion of the discrete, nonlinear elastic field. The first three terms in the expansion are typically (1) linearised elasticity, (2) nonlinear elasticity, (3) strain-gradient elasticity. This yields high accuracy simulation results with small computational domains, e.g., in the following figure for a screw dislocation (bcc, W, 111, EAM); see [73], [48] for more details.

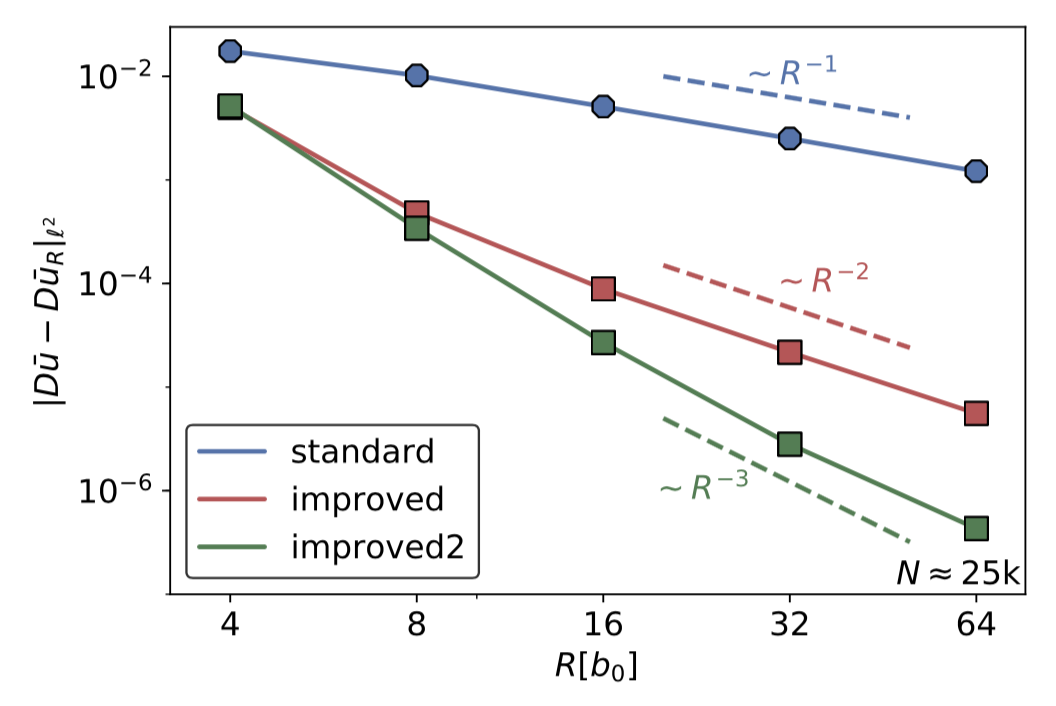
It is particular interesting though (work in progress) to explore higher-order generalisations as well as applications to electronic structure models.