Nowadays, I spend most of my time on hybrid mechanistic/machine-learned interaction models for atoms and molecules, but am interested in many other topics as well (see below). My research on this topic straddles rigorous analysis and numerical analysis, scientific computing (algorithms), modelling and applications primarily in molecular modelling (usually with collaborators). In particular, for students interested in working with me, there is a lot of flexibility in what branches of my research programme to engage.
Hybrid Mechanistic & Data-driven Modelling
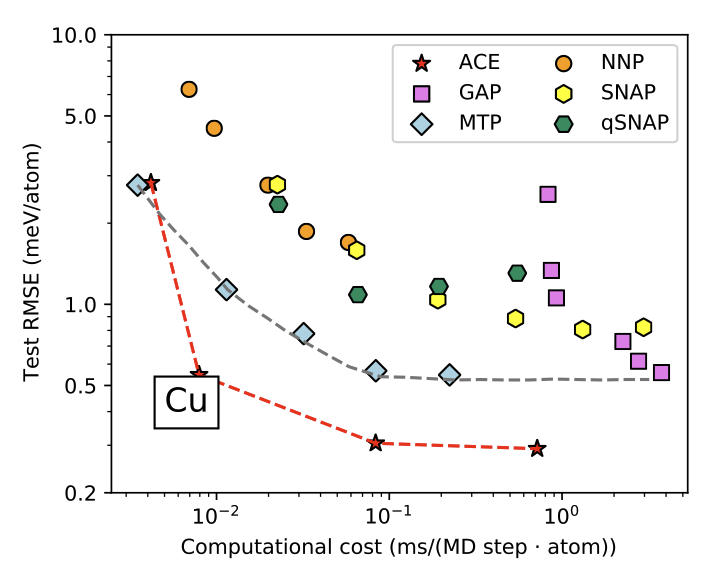
Atomistic modelling and simulation requires efficient computation of energies and forces. Machine learning (ML) based surrogate models parameterized to large data sets of reference electronic structure calculations, have proven particularly successful in recent years. In my group, our focus is on analytical and numerical aspects, both new methodology and theoretical foundations.

Material Defects
Many material defect simulations, including multi-scale schemes (A/C, QM/MM, . . .) can be understood within a single framework: a coarse model for a far-field provides a boundary condition for a core region of interest. Our work focuses on understanding this connection, which leads to mathematically rigorous models of defect mechanics, derivation of improved boundary conditions, as well as new algorithms for material defect simulation.
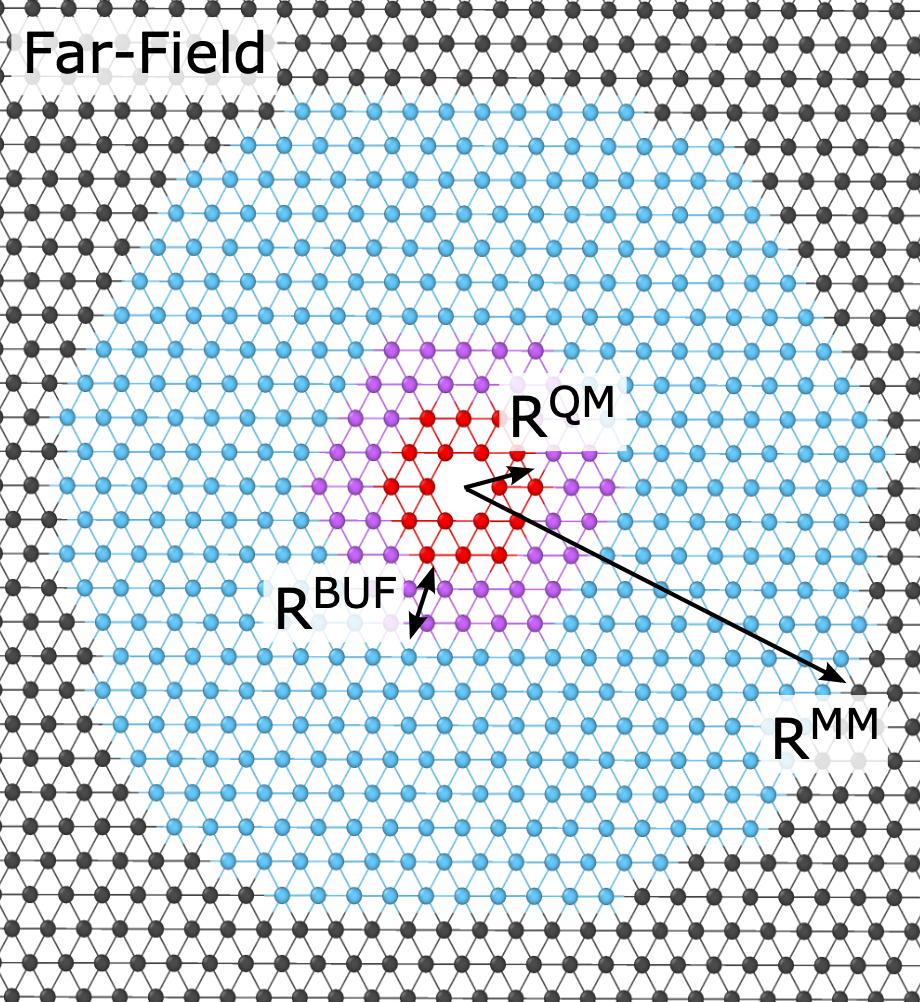
QM/MM Multiscale Methods
QM/MM methods are concurrent multi-scale methods: Regions of interest, such as a dislocation core are modelled with an electronic structure model, while the material bulk is modelled with a computationally inexpensive interatomic potential model. Our research focuses on the question how QM/MM methods can be constructed in a way that guarantees convergence with increasing QM region size.
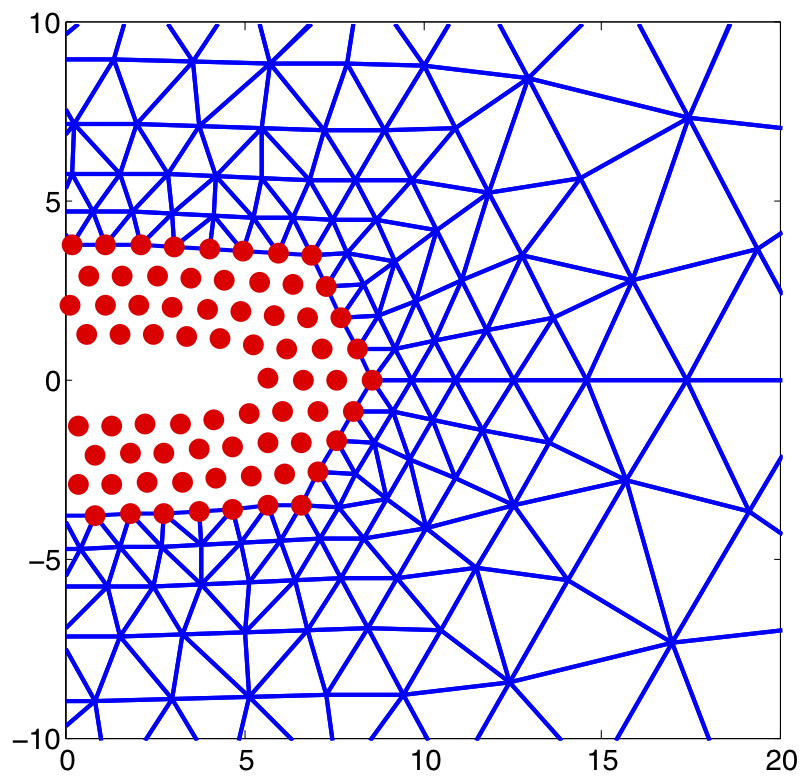
Atomistic/Continuum Coupling
Atomistic/continuum coupling methods are intended to enable extremely large-scale atomistic simulations in scenarios where there are extended regions of the atomistic configuration that behave essentially as a continuum. In the past I have worked extensively on the numerical analysis foundations for those methods.
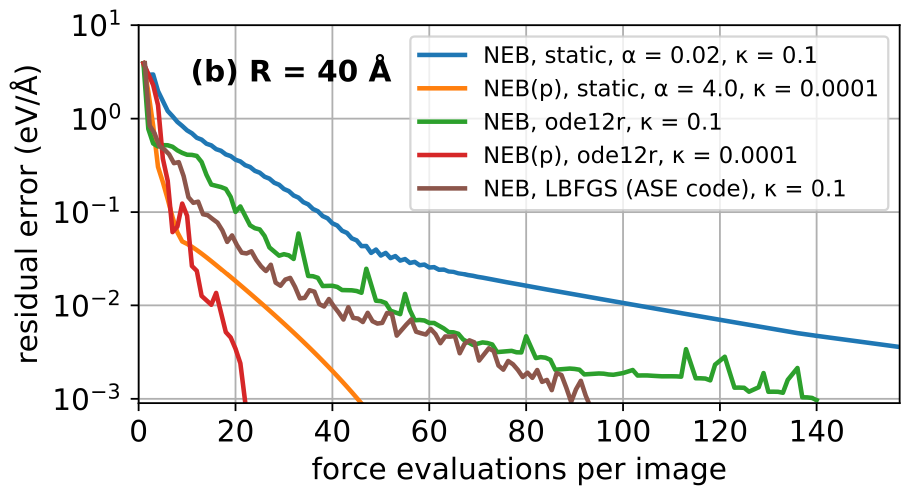
Optimisation for Molecular Simulation
I have been developing bespoke algorithms for molecular geometry optimisation. The main thrusts of this research are (1) preconditioners for potential energy landscapes to accelerate convergence; (2) effective line-search heuristics; (3) saddle point search (e.g., dimer method); and (4) transition path search (e.g. NEB). Especially (3, 4) also lead to very nice (unsolved) questions for mathematics / numerical analysis.
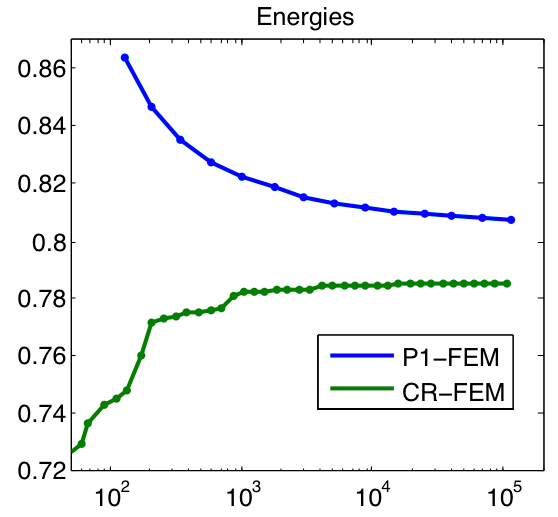
Lavrentiev GAP Phenomenon
The Lavrentiev gap phenomenon is the property of certain variational problems the infimum of the energy taken over Lipschitz functions can be strictly larger than the infimum taken over the entire admissible class. This means, in particular, that conforming finite element methods are incapable of detecting the global minimizers and leads to some very interesting challenges for numerical analysis.
I also work, or have worked, on the following topics:
Adaptive finite element methods for phase field models of fracture
Phase field models for dynamic crack propagation
Griffith model for fracture
Discontinuous Galerkin finite element methods
Gradient flows, in particular nonlinear viscoelasticity
Convergence of adaptive finite element methods
Numerical enclosure methods
Optimal control