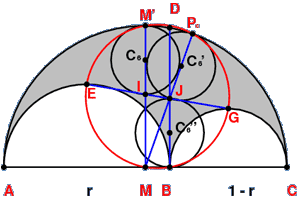
arbelos   What is an arbelos? Properties of an arbelos         Distances and areas         Archimedes' circles         Apollonius circle         Bankoff circle         Pappus chain References   Stephen Tan 42373027 Dec 16, 2005 Math 308 by Dr. Bill Casselman Final Project Page 10 Let B be the point at the notch of the arbelos, and D directly above it on the enclosing semicircle. Let MM' be a perpendicular bisector of AC, and let E and G be points sitting at the top of the interior semicircles.   Let EG intersect MM' and BC at I and J respectively. Then circles C6 - passing through I and tangent to arc AC at M' - and C6' - passing through J and tangent to arc AC at Pc - and C6'' - passing through J and tangent to AC at B - are all Archimedean circles. The circle C6'' is also known as a Bankoff circle. 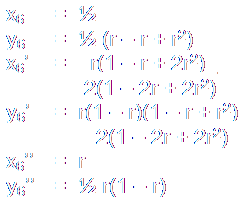The centers of C6, C6', C6'' are given by Rather amazing, E, M, B, G, Pc, D, and M' are concyclic in a circle with center at ((1 + 2r)/4 , 1/4) and radius
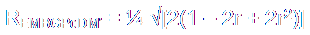