Dr. Neil Balmforth
RESEARCH INTERESTS
Pattern Formation In Systems With Continuous Spectra And Fluid Shear Flows:
Theories of pattern formation may explain phenomena as diverse as the form of living organisms, the structure of a crystal and the meander of a river. However, most theories deal with systems in which patterns form as a result of the appearance of a small of number of 'modes' of instability (that is, one simple type of pattern, such as a hexagonal convection cell in a heated fluid). These are the eigenmodes of the linear stability problem and provide a natural set of tools to describe the forming patterns. My research extends some of these ideas to systems with a continuous eigenvalue spectrum, for which the usual pattern theories fail. Notable examples of such system are inviscid shear flows and vortices, and instabilities in ideal plasmas. In these contexts, reduced models can be developed to describe the "bifurcation to instability from the continuous spectrum". The theory is relevant to laboratory experiments with confined electron plasma, and to transport and mixing in ocean and atmosphere. In astrophysics, shear flows occur in accretion disks and differentially rotating stellar interiors. Here, for example, related techniques can be used to explore how much angular momentum can be transferred between a proto-planet and its immediate gaseous environment, which has important ramifications on orbital migration and evolution of these planetary precursors.
Some longstanding collaborators are Phil Morrison and Bill Young, although Jean-Luc Thiffeault deserves an honourable mention.
A review
of a lot of it
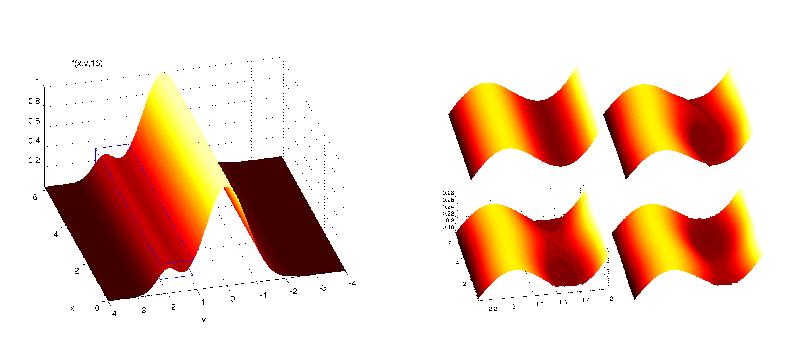
(Shown is the distribution function as a surface above the space-velocity plane; the distribution rolls up into an "electron hole" in the vicinity of the bump on tail)
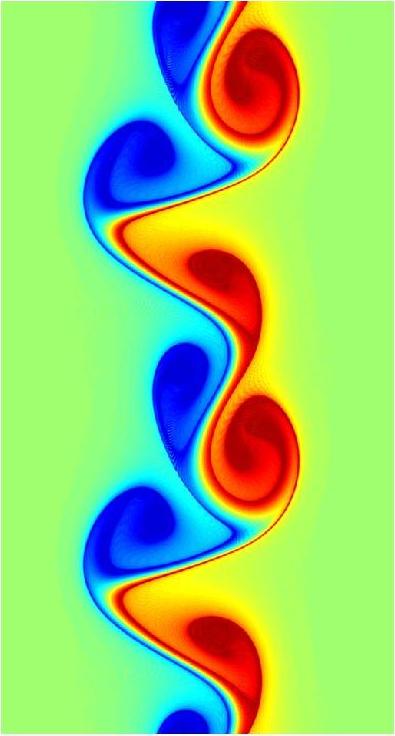
(colourmap of vorticity after instability induces the jet to meander and break up into vortices)
(shown are colourmaps of the evolving potential vorticity or "vortensity" in a narrow strip surrounding the "co-rotation" radius)