Method of Approximation

In order to model how light rays bend and refract in our eyes, we can perform step-by-step ray tracing. In this section, I'll attempt to explain how these pictures were modelled by going through the step-by-step ray tracing method.

Snell's Law and Refraction
When dealing with light and refraction, the basic physical law that we appeal to is Snell's Law. Snell's Law relates the incoming angle of the light ray with its new refracted angle once it goes into another medium:
ni sin i = nr sin r

where:
ni = the index of refraction for the medium that the light begins in
i = the incident angle (in degrees)
nr = the index of refraction for the medium the light is entering
r = the refracted angle (in degrees)
This diagram below sketches a picture of the system that we are looking at. Notice that the angle of incidence and refraction are both relative to the line perpendicular (or normal) to the surface (the dashed line). The solid black line represents the ray of light as it strikes the grey shaded lens. The refracted ray is coloured blue, and the green line represents the ray of light if it has travelled straight through without being changed. As you can see, the ray of line bends "inward" towards the normal, and angle r is smaller than i is. This is a general behaviour of lens which have this convex shape. It turns out that concave lens have the reverse property; when going into materials with higher indices of refraction, convex lens tend to bend outward.


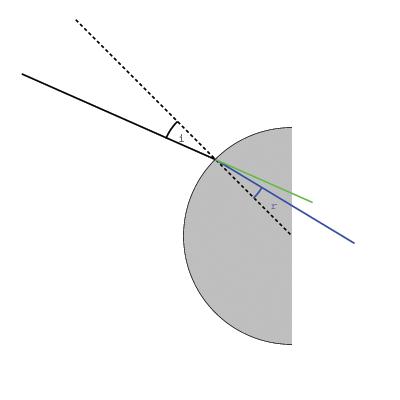
When tracing the ray through the different interfaces, the same fomula is used over and over again. This generates the pictures as they were used in the project.

Lens Shapes

In order to simplfy the calculations for this project, the lens that were used (both the eye and the corrective lens) are assumed to be spherical. A spherical lens is formed in the following way:



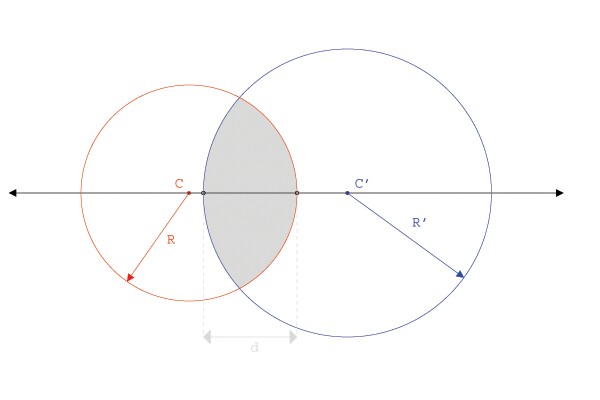
The lens has two surfaces, both of which can be approximated as being the soild that results from the intersection of two spheres. The two intersecting spheres, with radii R and R' have two centers located at C and C' respectively. In the next section, we will discuss how variations in the distance between C and C' effect the distance, d, and the effect it has on lens focusing.

Introduction
Colour Vision
Colour Math
Approximations
Focal Lengths and Distances
GRIN Systems
Human Vision
Vision Problems
Corrections