Colour "Math"
and Its Equations
In combining various amounts of red, green, and blue we can generate a
variety of colours, as the picture below clearly shows. It turns out
that we can express these colours in terms of some equations.
It turns out that a very simple treatment of this addition colour
method describes fairly accurately how we see the world. We can see from
the picture that there are a few basic equations:
Blue +Red =Magenta
Red + Green =Yellow
Green +Blue = Cyan
Blue +Red + Green =White
From this, we also have other equations that we can also derive other
"colour equations".
For example, what would happen if
added magenta and yellow together?
Magenta is made up of Blue and Red.
Yellow is made up of Red and Green.
The net result is: (Blue + Red)
+ (Green + Red)
= (Blue + Red + Green)
+ (Red)
= White + Red
The colour we see should be a combination of White, Red and their mixture
which is Pink.
What would happen
if you had white light, and you had a filter that could absorbed all the
blue light?
White is made up of Blue +Red + Green
Take away "Blue" from both sides of the
equation, and we get:
White - Blue = Red + Green = Yellow
The colour we see should look something like Yellow.
When two colours
together make white, they are called complementary. Yellow and blue are
considered complementary, since when they mix together, they will make
white light. As these "equations" show, we can think of
colour as being made up as a sum of each of the three components:
A
(Blue) + B (Red) + C (Green) = Total Colour
where A, B, and C
describe that total amount of each colour that we see.
When using a
computer, each colour uses a value between 0 and 255 inclusive for each
of green, red, and blue. Each of these number assigns a certain
"deepness" or saturation for that colour. A colour is defined as saturated when there is only that
mixture of light and there is no white light possible. For
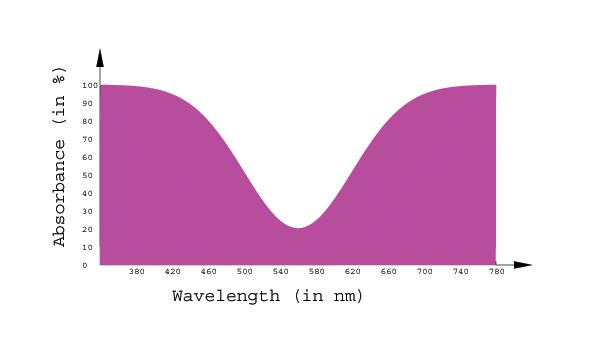
example, the curve of magenta on the left is considered saturated. There
are "red" and "blue" wavelengths being absorbed, but there is no white
in the colour, since there is no (or very little) green being absorbed
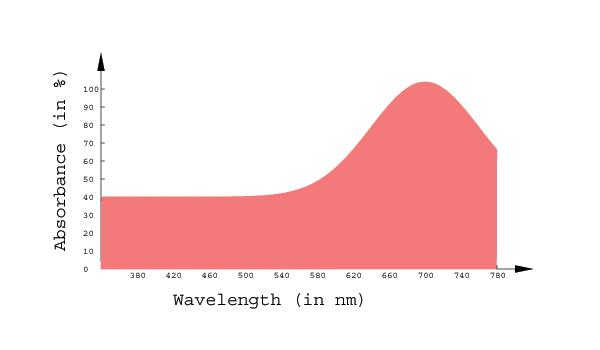
to make white. On the right, there is absorbance curve for pink. Notice
that there are considerable amounts of blue, green and red being
absorbed; this mean that the resultant colour will have a layer of
white. Since the remaining colour is red, the mixture of red and white
is the familiar pink.
If we recall the
image of the overlaid absorbances, it turns out that there doesn't
appear to be a region were there is only one colour that absorbed. As
such, we as humans can only see "near-saturated" colours. It turns out
that even at the very fringes of the spectrum near the ultra-violet and
infared red, each of the pigments still absorbs a tiny bit, which
slightly washes out the colour that we see.
Now that we understand how we see colour, the next section will discuss
how we see in general. In this next part, it takes a much more
technical twist.
Introduction
Colour Vision
Colour Math
Approximations
Focal Lengths and
Distances
GRIN Systems
Human
Vision
Vision Problems
Corrections
