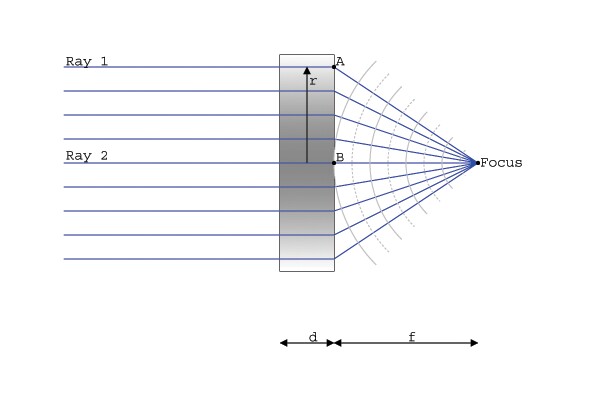
GRIN
Systems
GRIN stands for
GRadient INdex, and refers to variations in the index of refraction in
the lens. Even using a flat lens, you can still have parallel rays from
a source focus at a common point. It turns out that the center of the
lens has the highest index of refraction, and as you move out from the
center, the index decreases. A front view of a lens would resemble the
lens on the left. The image of the right is a side view of how the light
rays bend to the common focus, f,
through a lens of thickness, d.

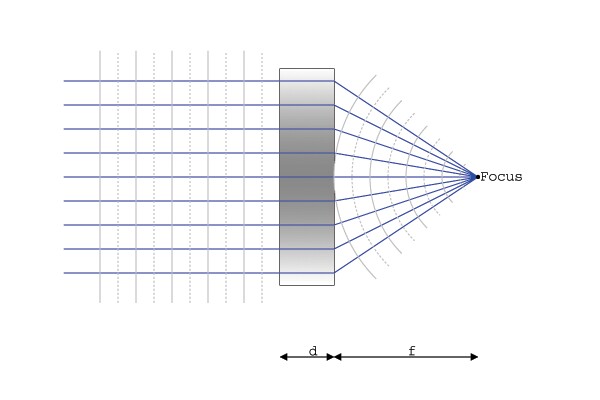
It turns out that
parallel light waves coming in from the left hand side are refracted
into a spherical pattern when they exit. This allows them to come
together at a common focus, similar with other curved lenses that were
introduced previously. The lens in our eye has a maximum index of
refraction of approximately 1.406 in the middle, and 1.386 towards the
outside. This gives our eye more "focusing power" because even slight
variations in thickness also effect the way in which the index variation
is distributed.
In this case, we
will take an in-depth look into how a a flat lens can focus as in the
above pictures. First off, let's begin with the necessary labels:
The major goal is to
have all the light sources pass through the lens and meet at the focus
at the same time. Here, we have selected two different rays. Ray 2
travels right through the center of the lens, and Ray 1 travels slightly
outside of the center. As you can see from the picture, the Ray 1 has to
travel a longer distance than Ray 2 does. By making the index of
refraction higher in the middle, it slows down Ray 2 so that Ray 1 can
travel the additional distance required. In the following equation, we
relate the two by measuring the time it takes them to travel through the
lens, and then to the focus.
Ray 2 travels
through the lens, and then goes from Point B to the Focus through
(presumably) air. The time it takes is:
Total Time = (Time through Lens) + (Time
After Lens to Focus)
= (NMAX) d + (NAIR)
f
where:
d is the thickness of the lens
f is the focal length
NMAX is the index at the center (which is where is reaches a
maximum)
NAIR is the index of refraction in wait
Ray 1 does something
very similar. It travels through the lens at a point with a smaller
different index of refraction, but a longer length from the lens to the
focus.
Total Time = (Time through Lens) + (Time
After Lens to Focus)
= (NR) d + (NAIR)
(Distance from A to F)
where:
d,f, and NAIR are the same as above
r is the distance of the ray from the central axis
NR is
the index of refraction at a distance r
Since AB and the Focus form a right triangle, we can use Pythagoras'
Theorem. We can replace the (Distance from A to F) with what Pythagoras'
Theorem gives us:
(NR) d + (NAIR)
(Distance from A to F) = (NR) d + (NAIR)
[ sqrt ( r2 + f2 )]
At this point,
we can compare the two equations, and try to solve to NR as a
function of the other variables. In order to make it more viewable, the
two sides of the equation have been coloured.
Ray 2 = Ray 1
(NMAX) d + (NAIR) f =(NR) d + (NAIR) [ sqrt ( r2 + f2
)]
(NMAX) d + (NAIR)
f - (NAIR) [ sqrt ( r2 + f2 )] = (NR) d
(NMAX) d + (NAIR) [ f - { sqrt ( r2 + f2
) } ] = (NR) d
NR = (NMAX) + (NAIR/d) [ f - { sqrt ( r2 + f2
) } ]
In order to simplify
the look of the equation, we will assume that NAIR = 1. This
is a fair assumption, since the actual value of NAIR is around
1.00029 for light with a wavelength of 589 nm. Also, since term
involving the square root [ f - { sqrt ( r2
+ f2 ) } ] is a negative
quantity, it is easier to reverse the order, and add a negative sign.
NR = (NMAX) - (1/d) [ { sqrt ( r2 + f2 )
} - f ]
There is one last
change that can be made; the rather confusing portion of the right hand
side can be simplified. By using Newton's Binomial Theorem, we can make
an approximation that the part in the right-hand square bracket is equal
to a much simpler expression:
NR =(NMAX) - (r2/2fd)